原文链接:https://mp.weixin.qq.com/s/sYjzK7OiQOzpRCJJPKtllg
来源: 集智俱乐部

苏联数学家柯尔莫哥洛夫(Andrey N. Kolmogorov,1903-1987)。图源:https://wolffund.org.il/
编者按
大模型向计算理论提出了新问题,而计算理论也可帮助大模型揭示第一性原理,从而找到边界和方向。例如,苏联数学家柯尔莫哥洛夫和学生阿诺德在20世纪50年代完成的KA叠加定理。
尼克| 作者
陈晓雪| 编辑
赛先生|来源
今年五一假期,麻省理工学院物理学家Max Tegmark和其博士生刘子鸣等人在arxiv上挂出的一篇关于机器学习的文章引发关注。他们提出了一种叫做KAN (Kolmogorov-Arnold Network) 的新框架,称其在准确性和可解释性方面的表现均优于多层感知器 (MLP) 。
今天,我们就来谈谈柯尔莫哥洛夫-阿诺德叠加定理的源起和发展。在之前的文章“”,笔者曾经简要介绍过过柯尔莫哥洛夫 (A. N. Kolmogorov,1903-1987) 和阿诺德 (Vladimir Arnold,1937-2010) 的其他工作。
万能的苏联数学家柯尔莫哥洛夫对计算机科学有两大贡献。首先,他和美国数学家所罗门诺夫和蔡廷独立发展的所罗门诺夫-柯尔莫哥洛夫-蔡廷理论 (大多数时间被更简单地称为柯尔莫哥洛夫复杂性,或算法信息论) 正在成为大语言模型的理论基础和解释工具。追随柯尔莫哥洛夫做复杂性研究的学生列文 (Leonid Levin,1948-) ,独立于库克 (Stephen Cook,1939-) ,在1970年代初期得出了NP-完全性的结果,2000年后这个原以库克为名的定理,在计算理论的教科书里多被改称为库克-列文定理。列文虽没有像库克那样得到计算机科学的最高奖图灵奖,但得了ACM和IEEE联合颁发的高德纳 (Knuth) 奖,算是补偿。
柯尔莫哥洛夫的另一重要贡献在数学界影响广泛,但很晚才被计算机科学家和人工智能学者赏识,尽管这项工作出现更早。他和学生弗拉基米尔·阿诺德在1956-1957年间共同证明的表示定理或称叠加 (superposition) 定理,后来成为神经网络的理论基础。神经网络复兴的数学保障是通用逼近定理 (universal approximation theorem) ,其源头就是柯尔莫哥洛夫-阿诺德叠加。就像柯尔莫哥洛夫的很多工作,都是他先开头指明方向,并且给出证明的思路或者证明的速写版,然后由学生们精化为完美的素描。
柯尔莫哥洛夫的另一重要工作KAM理论,也是和阿诺德合作完成的。阿诺德和以色列逻辑学家谢乐赫分享 (Saharon Shelah) 了2001年的沃尔夫奖,和另一位俄国数学物理学家法捷耶夫分享了2008年的邵逸夫奖。丘成桐公允地说,在亚历山德罗夫和柯尔莫哥洛夫等领导下的俄罗斯数学学派,当时已经接近美国数学的总体水平。其中犹太裔数学家群体的故事,现在读来,励志且令人唏嘘。
以ChatGPT代表的大语言模型引发的讨论,多聚焦于数据与算力等工程问题,理论方面的研究则不那么热烈。大模型向计算理论提出了新问题,而计算理论也可帮助大模型示第一性原理,从而找到边界和方向。在当下的理论没法解释工程实践时,工程师们也会转向历史去寻找前辈们被埋没的思想,力图为何去何从提供方向性的洞见。
早期神经网络的发展
神经网络作为大脑启发 (Brain-inspired) 的计算模型,始于麦卡洛克 (Warren McCulloch, 1898-1969) 和皮茨 (Walter Pitts,1923-1969) 1943年的工作。两位作者之一的皮茨是自学成才的逻辑学家,而麦卡洛克是神经心理学家,是皮茨老师辈的人物,他们提出神经元有一个阈值,即刺激必须超过这个阈值才能产生脉冲。虽然二人没有引用图灵和丘奇 (Alonzo Church) 在1936-1937年的论文,但在文中明确提出,只要给他们的网络提供无穷存储,他们的网络可以模拟λ-演算和图灵机。
随后相关的研究不断。丘奇的学生克莱尼 (Stephen Cole Kleene,1909-1994) 1956年进一步研究了McCulloch-Pitts 网络的表达能力。各种激活函数的选择是门艺术。McCulloch-Pitts 网络是离散的,更特定地说,是布尔值的,非0即1。现代的神经网络激活函数大多是非线性的,不局限于布尔值。可以说,McCulloch-Pitts 网络更像是布尔电路,而不是现代意义的神经网络。
弗兰克·罗森布拉特(Frank Rosenblatt)提出的“感知机” (Perceptron) 是1950年代神经网络的标志性工作。罗森布拉特是心理学出身,1957年在一台IBM 704机上实现了单层“感知机”神经网络,证明了感知机可以处理线性可分的模式识别问题,随后又做了若干心理学实验,力图证明感知机有学习能力。罗森布拉特1962年出了本书《神经动力学原理:感知机和大脑机制的理论》 (Principles of Neurodynamics: Perceptrons and the Theory of Brain Mechanisms) ,总结了他的所有研究成果,一时成为神经网络派的必读书。罗森布拉特的名声越来越大,得到的研究经费也越来越多。美国国防部和海军都资助了他的研究。罗森布拉特一改往日的害羞,成了明星,频频在媒体出镜,开跑车,弹钢琴,到处显摆。几乎每个时代都有媒体需要的具有娱乐潜质的科技代表人物。媒体对罗森布拉特也表现出了过度的热情。毕竟,能够构建一台可以模拟大脑的机器,当然值一个头版头条。这使得另一派的人相当不爽。

罗森布拉特和他的感知机(Frank Rosenblatt,1928-1971)。图源:维基百科
明斯基 (Marvin Minsky) 是人工智能的奠基人之一,也是,这个会议定义了“人工智能”这个词,并把神经网络也纳入人工智能的研究范围。早期明斯基是神经网络的支持者。他1954年在普林斯顿大学的博士论文题目是《神经-模拟强化系统的理论及其在大脑模型-问题上的应用》,实际上就是一篇关于神经网络的论文。但他后来改变了立场,认为神经网络并不是解决人工智能问题的有效工具。他晚年接受采访时开玩笑说,那篇300多页的博士论文从来没有正式发表过,大概只印了三本,他自己也记不清内容了。貌似想极力开脱自己和神经网络学科的关系。
明斯基和罗森布拉特是中学同学,他们均在纽约的布朗克斯 (Bronx) 科学高中就读。这所学校大概是全世界智力最密集的高中之一,毕业生里出过9个诺贝尔奖、6个普利策奖和2个图灵奖。明斯基是1945年的毕业生,而罗森布拉特是1946年的毕业生。他们彼此认识,互相嫉妒。
一次会议上,明斯基和罗森布拉特大吵了一架。随后,明斯基和麻省理工学院的教授佩珀特 (Seymour Papert) 合作,证明罗森布拉特的感知机网络不能解决XOR (异或) 问题。异或是一个基本的逻辑问题,如果连这个问题都解决不了,那意味着神经网络的计算能力实在有限。明斯基和佩珀特把合作成果写成书:《感知机:计算几何学导论》 (Perceptrons: An Introduction to Computational Geometry) ,这书影响巨大,几乎否定了整个神经网络研究。

明斯基(Marvin Minsky,1927-2016)。图源:维基百科
其实罗森布拉特此前也已预感到感知机存在局限,特别是在“符号处理”方面,并以自己神经心理学家的经验指出,某些大脑受到伤害的人也不能处理符号。但感知机的缺陷被明斯基以一种敌意的方式呈现出来,对罗森布拉特是个致命打击。最终,政府资助机构也逐渐停止对神经网络研究的支持。1971年,罗森布拉特在43岁生日那天划船时溺亡,有说法认为这是自杀。


罗森布拉特和明斯基各自题为《感知机》的著作。
希尔伯特第13问题与神经网络
要想理解AlphaFold3进步的意义,需要了解生物体包含了多个层次的复杂性。生物的运行蓝图从DNA经由转录得到RNA,再由RNA翻译生成蛋白质,蛋白在生成后会进行修饰 (蛋白质产生后发生的化学变化) ,并经由与小分子配体 (ligand) 和离子,以及蛋白质之间的互作共同影响,执行特定的功能。
大卫·希尔伯特1900年在第二届国际数学家大会提出了23个待解数学问题,这些问题指引了后续的数学发展。希尔伯特提出的第13个问题,相较于其他问题,并不是特别引人注目,即使在数学家群体中,也远非广为人知。我们用线上搜索引擎Google Ngram比较一下第10和第13问题,可知大概。
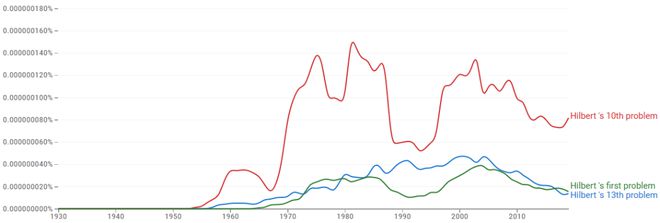
Google Ngram的结果
希尔伯特第13问题是这样说的:7次方程的解,能否用两个变量的函数的组合表示? (Impossibility of the solution of the general equation of the 7-th degree by means of functions of only two arguments) 。希尔伯特的猜测是不能。
我们知道5次以上的方程是没有求根公式的。但一元5次和6次方程可以分别变换为:
x5 + ax + 1 = 0,
x6 + ax2 + bx +1 = 0
爱尔兰数学家哈密尔顿1836年证明7次方程可以通过变换简化为:
x7+ax3+bx2+cx+1=0
解表示为系数a,b,c的函数,即x=f(a, b, c)。希尔伯特第13问题就是问这个三元函数是否可以表示为二元函数的组合。
在罗森布拉特做感知机(Perceptron)的同时,柯尔莫哥洛夫和阿诺德正在研究“叠加”问题。柯尔莫哥洛夫1956年首先证明任意多元函数可用有限个三元函数叠加构成。阿诺德在此基础上证明两元足矣。他们的成果被称为柯尔莫哥洛夫-阿诺德表示定理,或柯尔莫哥洛夫叠加定理,有时也被称为阿诺德-柯尔莫哥洛夫叠加(AK叠加),因为是阿诺德完成了最后的临门一脚。本文中以下统称KA叠加定理或KA表示定理。柯尔莫哥洛夫的本意不完全是为了解决希尔伯特第13问题,但叠加定理事实上构成了对希尔伯特对第13问题原来猜测的(基本)否定。再后阿诺德和日本数学家志村五郎合作在这个问题上进一步推进。

1973年,柯尔莫哥洛夫在准备自己的报告。图源:维基百科
至于是否柯尔莫哥洛夫和阿诺德“叠加”是希尔伯特第13问题的彻底解决,数学界有不同看法,有些数学家们认为希尔伯特原来说的是代数函数,而柯尔莫哥洛夫和阿诺德证明的是连续函数。希尔伯特的原话是“连续函数”,但考虑到黎曼-克莱因-希尔伯特的传统,数学家们认为希尔伯特的本意是代数函数。希尔伯特第13问题的研究并没有因为KA叠加定理完结,而是还在继续,这超出了本文范围。无论如何,叠加定理,歪打正着,为后续神经网络研究奠定了理论基础。

阿诺德(Vladimir Arnold,1937-2010)。图源:维基百科
把KA叠加定理和神经网络联系起来的是一位数学家出身的企业家。赫克-尼尔森 (Robert Hecht-Nielsen,1947-2019) 一直是神经网络的坚信者。他1986年创办了以自己名字命名的软件公司HNC,专事信用卡反欺诈。他把公司的核心技术赌在神经网络,当时正是神经网络的低潮期,需要极大的勇气和远见。2002年公司被最大的信用评级公司Fair Issac以8.1亿美金收购。1987年,赫克-尼尔森在第一届神经网络大会 (ICNN,后改名为神经网络联合大会IJCNN) 上发表文章,证明可以用三层神经网络实现柯尔莫哥洛夫-阿诺德叠加。这篇文章很短,只有三页纸,但却令人脑洞大开。这个结果在理论上给神经网络研究带来了慰藉,并激发了一系列有趣的数学和理论计算机科学的研究。
KA叠加定理如下:
即,任意多元的连续函数都可以表示为若干一元函数和加法的叠加。加法是唯一的二元函数。简单的函数都可以通过加法和一元函数叠加而成,这个道理并不难理解,如下所示,减、乘、除可由加法叠加而成:
a − b = a + (−b),
a · b = 1 /4 ((a + b) 2 − (a − b) 2) ,
a /b = a · 1/ b
所有的初等运算都可以通过一元运算和加法完成。在这个意义上,加法是通用的 (universal) ,用加法叠加做其他运算时并不需增加额外的维度。
赫克-尼尔森指出,KA叠加定理可以通过两层网络实现,每层实现叠加中的一个加号。他干脆就把这个实现网络称为“柯尔莫哥洛夫网络”。法国数学家卡汉(Jean-Pierre Kahane,1926-2017),在1975年改进了KA叠加定理,如下:
其中,h被进一步限制为严格单调函数,lp是小于1的正常量。


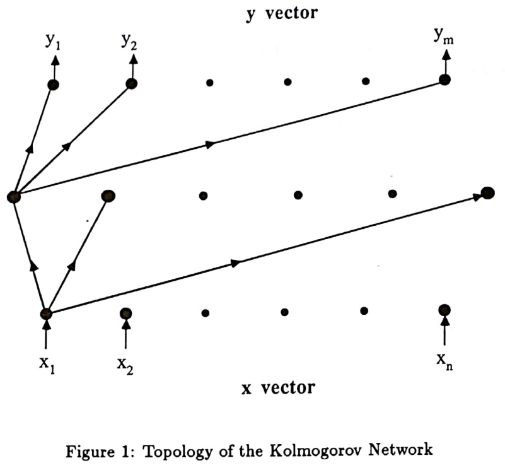
赫克-尼尔森(Robert Hecht-Nielsen,1947-2019)和1987年论文及插图
另一位也是数学出身的工学教授赛本科 (George Cybenko) ,稍后在1988年证明了有两个隐层且具sigmoid激活函数的神经网络可以逼近任意连续函数。赛本科的文章更具细节和证明。虽然赛本科没有引用Hecht-Nielsen-1986,但引用了Kolmogorov-1957。我们不知道他是否受到了赫克-尼尔森的启发。而几乎同时的独立工作如Hornik-1989,都是既引用Kolmogorov也引用Hecht-Nielsen,可见赫克-尼尔森对揭示柯尔莫哥洛夫-阿诺德叠加的计算机科学涵义是先知先觉。这些相关的结论及各种变体和推广被统称为“通用逼近定理” (Universal Approximation Theorem) 。除了连续函数,也有人力图证明非连续函数也可以用三层神经网络逼近 (Ismailov,2022) 。无论如何,学过数学的总能从第一性原理出发来考虑问题。此后,明斯基导致的神经网络危机算是翻篇了。

George Cybenko。图源:https://engineering.dartmouth.edu/
赫克-尼尔森等的证明是存在性的而不是构造性的。计算机科学既是科学也是工程,一个思路是不是可行,必须得伴之以算法和实现,并且要有可靠的复杂性分析和工程演示。
1974年,哈佛大学的一篇统计学博士论文证明了神经网络的层数增加到三层,并且利用“反向传播” (back-propagation) 学习方法,就可以解决XOR问题。这篇论文的作者沃波斯 (Paul Werbos) ,后来得了IEEE神经网络学会的先驱奖。沃波斯这篇文章刚发表时,并没有在神经网络圈子里引起多少重视,主要原因是沃波斯的导师是社会学和政治学领域的,他想解决的问题也是统计学和社会科学的。把“反向传播”放到多层神经网络上就成了“深度学习”。
深度学习首先在语音和图像识别上取得突破,后来在强化学习的帮助下,又在博弈和自然语言处理方面得到惊人的成功。但深度学习的机制一直没有得到满意的解释。
Tomaso Poggio是英年早逝的计算机视觉研究者马尔 (David Marr) 的合作者。马尔在1980年去世后,Poggio的兴趣逐渐转向机器学习和神经网络的理论。许多数学家也被拉入,例如菲尔兹奖得主、长寿多产且兴趣广泛的数学家斯梅尔 (Stephen Smale) 。不过, Poggio并不认可KA叠加定理可以作为通用逼近网络的数学基础。他早在1989年就著文指出实现KA叠加的网络是不平滑的 (见Girosi & Poggio, 1989) 。在后续的工作中,他还指出维度灾难 (CoD) 取决于维度/平滑度。平滑度不好,自然会导致维度灾难。KA叠加定理虽有理论价值,但直接应用到实际的神经网络上,会碰到平滑性问题,于是工程上鲜有进展。KA叠加定理从此被遗忘。
到了今年5月,KA叠加定理又重新得到重视。麻省理工学院的物理学家和科普作家Max Tegmark,在主业宇宙学之外一直喜欢跟踪人工智能尤其是机器学习。他作为通讯作者、刘子鸣作为第一作者的最新文章就力图复活KA叠加定理。他们认为,原始的柯尔莫哥洛夫网络只有两层,如果把层数加深,把宽度拓广,也许可以克服平滑性的问题。他们把推广的网络称为KAN (Kolmogorov-Arnold Network) ,而事实上,赫克-尼尔森早就把实现KA叠加定理的网络称为Kolmogorov Network。

物理学家Max Tegmark。图源:维基百科
实现叠加定理的网络都可图示如下:
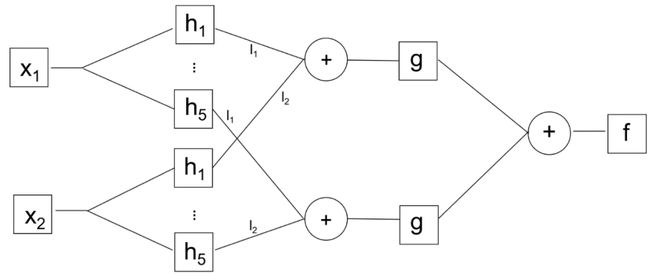
KAN的作者们自称的最关键的创新点之一,是把计算放在网络的边 (edge) 上而不是点 (node) 上,点上只执行加法运算,这样可以缩小网络的规模。因为叠加定理只需要加法 (二元的) 和一元函数,实现一元函数的点可以坍塌成为边,边就是点,点就是边,这一点并不令人惊奇。如上图,点h可以看成是连接输入x和g之前加法的边。KAN中的加法只能在点上实现,因为加法是二元的,需要两个输入。在这个意义上,KAN和多层感知器 (MLP) 没有本质区别。正常的网络中,边数是点数的平方级,网络规模的缩小是否真正带来计算量的减少,仍需理论和实验的共同探索。
KAN的另一创新之一是学习激活函数而不是学习权重。但学习函数比学习权重要困难得多。KAN中,激活函数是用B-spline来拟合的,B-spline的所有劣势自然也会被带进KAN中。如果学习激活函数的成本很高,网络就丧失了通用性 (universality) 。目前需要在工程实践中进一步证明KAN的优势。 但无论无何,KAN的工作鼓励我们从第一性原理出发去寻找新的路径,为解释提供数学依据。
一段历史和一个思想实验:第谷机器
启蒙运动后的思潮在理性主义和经验主义之间一拨一拨地迭代演进。科学亦如此。哥白尼毫无疑问是理性主义者,他的工具是数学。之后的开普勒也是理性主义者。但他们之间的第谷布拉赫却是彻头彻尾的经验主义者,他的工具是自制的各种测量仪器,他那时还没有望远镜。其身后留下24本观测数据,其中包含777颗恒星的星表。这批数据被开普勒继承。濒死的贵族第谷布拉赫已经和小肚鸡肠的开普勒几乎闹翻了。这段历史的简化版就是:哥白尼推翻了托勒密的地心说,代之以更简单的日心说。但第谷布拉赫并没有走得那么远,按照剑桥科学史家霍斯金的说法:第谷在哥白尼创新的地方保守,而在哥白尼保守的地方创新。他提出了准日心说:所有行星都绕着太阳转,但太阳带着行星们围着地球转。开普勒修正了第谷的工作,提出了行星运动三定律,工具就是数学。开普勒的工作得到伽利略的肯定。伽利略又是一个经验主义者,他有了更新的工具:望远镜。1609年,开普勒在《新天文学》中首先发表头两条定律的时候,伽利略刚造出3倍的望远镜。
第谷布拉赫自制的观测设备,按今天的标准看,都是些简陋的玩具。但,我们假设他除了那些设备之外,还有一台现代的先进的机器学习装备。为了方便,我们暂且称之为第谷机,这台学习机可以实现今天的深度学习和强化学习等各种机器学习算法。他可以把他那24大本记录数据喂给这台第谷机对之加以训练,训练好的第谷机就可以输出任意一个恒星和行星的轨道数据。若如此,日心说还是地心说还重要吗?反正第谷机能输出我们需要的数据。第谷机的表现,当时的人肯定难以解释,估计会称之为“涌现”。那我们可以说这个第谷机完成的功能是科学吗?它的行为可以解释吗?必须列出方程才能称之为解释吗?多么简单的方程才能称之为解释?这甚至可以影响我们做科学的方式,按照第谷机的机制,我们只是负责不停地收集数据,然后喂给机器,不断完善预测机制。如果牛顿之前就有了深度学习,那么是不是就不会有牛顿定律乃至相对论了?只有数值解而没有解析解的方程所描述的世界就不能被理解吗?不受限制的三体问题不能算被理解吗?
尾声
阿诺德除了对数学的技术内容做出深刻贡献,对数学哲学和数学史也有很多有趣的论断。他曾说:数学就是物理学中那些实验成本很低的部分 (Mathematics is the part of physics where experiments are cheap) 。我们也可以套用此话说,计算科学其实才是物理学中实验成本很低的部分。我们可以问:人类能够学习的东西比理性更多、更少还是一样?通用逼近定理似乎指向理性不会比可学习的更多。我们可以更加深入地探讨KA叠加定理的哲学蕴意。
阿诺德在接受采访时说:“布尔巴基学派 (Bourbakists) 声称所有伟大的数学家——用狄利克雷 (Peter Gustav Lejeune Dirichlet) 的话来讲——是‘用清晰的思想代替盲目的计算’。布尔巴基宣言中的这句话,翻译成俄语变成了‘用盲目的计算代替清晰的思想’,宣言的译审是柯尔莫哥洛夫,他精通法语。我发现这一错误后大吃一惊,就去找柯尔莫哥洛夫讨论。他答道:我不觉得翻译有什么问题,翻译把布尔巴基风格描述得比他们自己说的更准确。遗憾的是,庞加莱 (Henri Poincaré) 没在法国创建一个学派。”苏联数学家的毒舌和幽默别具一格。
当休谟说牛顿发现了物的定律时,他本意是想把牛顿拉到经验主义的阵营。但牛顿摒弃了机械论。我们力图说丘奇-图灵论题为心的定律 (实际上是“论题”) 。我们对人工智能的可解释性要求是基于机械论的。可解释性的目的是在法庭上给老百姓 (average person) 解释,而不是在最聪明的精英化之间形成共识。过去,科学的可解释性,是科学成功的标志。还原论 (reductionist) ,作为现代科学的传统,就是把一个难解的大问题还原为更小的、更原始且更易解释的小问题。机械论就是把所有运动都还原为某种碰撞,万有引力不需要碰撞,在机械论的角度就是不可解释的。而大模型则是把一堆以前不知是不是可解的小问题堆在一起打包解决,当整体问题被解决后,里面的小问题就不被人们认为是重要了。
我们可以说理性主义是“清晰的思想”,而黑盒子是“盲目的计算”。但物理定律一定比黑盒子更加经济吗?常说飞机不是学鸟,而是依靠流体力学,那是因为制造超级大鸟的成本太高。如果造鸟的成本低于求解流体力学方程,造鸟也许不是一个很坏的选择。Max Tegmark等试图用符号回归 (symbolic regression) 从数据中找出物理定律 (Undrescu & Tegmark) 。他的数据集之一是费曼《物理学讲义》中列出的公式。如果我们把学习看作是压缩,“盲目计算”有时可能比“清晰思想” (如符号回归或解析解) 的压缩比更高。科学问题在某种意义上成了经济学问题。也正是在这个意义上,计算机科学比物理学更加接近第一性原理,物理学不过是计算机科学的符号回归。
作者简介:
尼克,乌镇智库理事长。曾获吴文俊人工智能科技进步奖。中文著作包括《人工智能简史》《理解图灵》《UNIX内核剖析》和《哲学评书》等。
参考文献
[1]Liu, Z., Wang, Y., Vaidya, S., Ruehle, F., Halverson, J., Soljačić, M., ... & Tegmark, M. (2024). KAN: Kolmogorov-Arnold Networks. arXiv preprint arXiv:2404.19756.
[2]Cucker, F. & Smale, S. (2001), On the Mathematical Foundations of Learning, BULLETIN OF THE AMS, Volume 39, Number 1, Pages 1–49
[3]Cybenko, G. (1988), Continuous Valued Neural Networks with Two Hidden Layers are Sufficient, Technical Report, Department of Computer Science, Tufts University.
[4]Cybenko, G. (1989), Approximation by Superpositions of a Sigmoidal Function, Mathematics of Control, Signals, and Systems, 2(4), 303–314.
[5]Girosi, F. & Poggio, T. (1989), Representation properties of networks: Kolmogorov’s theorem is irrelevant, Neural Computation,1 (1989), 465–469.
[6]Hecht-Nielsen, R. (1987), Kolmogorov’s mapping neural network existence theorem, Proc. I987 IEEE Int. Conf. on Neural Networks, IEEE Press, New York, 1987, vol. 3, 11–14.
[7]Hilbert, D. (1900). Mathematische probleme. Nachr. Akad. Wiss. Gottingen, 290- 329. (“数学问题”,《数学与文化》北京大学出版社, 1990)
[8]Hornik, K. et al (1989), Multilayer Feedforward Networks are Universal Approximators, Neural Networks, Vol. 2, pp. 35Y-366, 1989.
[9]Ismailov, V. (2022), A three layer neural network can represent any multivariate function, 2012.03016.pdf (arxiv.org)
[10]Kahane, J. P. (1975), Sur le theoreme de superposition de Kolmogorov. J. Approx. Theory 13, 229-234.
[11]Kleene, S.C. (1956), Representation of Events in Nerve Nets and Finite Automata. Automata Studies, Editors: C.E. Shannon and J. McCarthy, Princeton University Press, p. 3-42, Princeton, N.J.
[12]Kolmogorov, A.N. (1957), On the representation of continuous functions of many variables by superposition of continuous functions of one variable and addition, (Russian), Dokl. Akad. Nauk SSSR 114, 953–956.
[13]Kolmogorov, A.N. (1988), How I became a mathematician, (姚芳等编译,我是怎么成为数学家的,大连理工大学出版社,2023)
[14]W. S. McCulloch, W. Pitts. (1943), A Logical Calculus of Ideas Immanent in Nervous Activity. Bulletin of Mathematical Biophysics, Vol. 5, p. 115-133.
[15]Poggio, T. & Smale, S. (2003), The Mathematics of Learning: Dealing with Data, NOTICES OF THE AMS
[16]Togelius, J. & Georgios N. Yannakakis, Choose Your Weapon: Survival Strategies for Depressed AI Academics, [2304.06035] (arxiv.org)
[17]Udrescu, Silviu-Marian & M. Tegmark (2020), AI Feynman: a Physics-Inspired Method for Symbolic Regression, arxiv
[18]尼克 (2021), 人工智能简史, 第2版.