原文链接:https://www.toutiao.com/article/7290804188861235753/?
量子位 | 公众号 QbitAI
基于博弈论,MIT提出了一种新的大模型优化策略。
在其加持之下,7B参数的Llama在多个数据集上超越了540B的“谷歌版GPT”PaLM。
而且整个过程无需对模型进行额外训练,消耗的算力资源更低。

这种基于博弈论制定的优化策略被称为均衡排名(Equilibrium Ranking)。
研究团队将大模型语言解码过程转化为正则化不完全信息博弈。
这个词可以拆解成“正则化”和“不完全信息博弈”两部分,我们将在原理详解部分展开介绍。
在博弈过程中,模型不断对生产的答案进行优化,让生成结果更加符合事实。
实验结果表明,在多个测试数据集上,均衡排名优化方式的效果显著优于其他方式,甚至其他模型。
那么,均衡排序方法具体是如何将博弈论应用到大模型当中的呢?
让大模型“自我博弈”
前面提到,研究人员将大模型进行语言解码的过程直接变成了“正则化不完全信息博弈”过程。
不完全信息博弈是整个方法的核心,正则化则是一种避免出错的机制,我们先来看这种博弈。
具体而言,他们设计了生成器(G)和判别器(D)两个模块,它们掌握着不同的信息,扮演不同角色。
生成器根据环境(N)随机给出的“正确性参数”生成答案;判别器则只负责判断生成器的答案是否正确,而不看环境参数。
如果判别器的判断与环境参数一致,两者都得到1分奖励,否则都不得分。

在执行重复的生成和判别当中,模型的目标是达到纳什均衡。
在纳什均衡策略组合下单方面改变自己的策略,而其他玩家策略不变,都不会提高自身的收益。
举个例子,张三和李四一起决定晚餐吃什么,选项有火锅和烧烤,其他已知条件如下:
张三对火锅的满意度是2分(很喜欢),对烧烤的满意度为1分(还可以)
李四对烧烤的满意度是2分,对火锅的满意度为1分
两个人都不想自己单独吃饭,因此单独吃饭时满意度均为0分
此时,两人的选择共有四种方式,对应的满意度得分如下表:

这一情境下,两人选择相同时即为最佳策略,此时只要任何一个人单方面改变策略,两人的满意度将同时变为0。
回到均衡排名优化法当中,生成器和判别器会先初始化策略,二者的依据分别基于问题或答案。
这一环境下的纳什均衡如下表所示:

初始化完成后,生成器和判别器会进行多轮博弈,逐步更新策略,直到迭代终止。
每一次博弈结束后,分别计算判别器和生成器的得分和最优策略得分的差值,称为“后悔值”。
然后逐步进行迭代,直到后悔值收敛,逼近纳什均衡。
达到纳什均衡后,生成器和判别器的策略便确定,会分别对候选答案进行打分,然后进行排序选出最佳答案。
在纳什均衡条件下,二者的评分应当是一致的,如果不一致,答案便会被剔除。

不过由于给生成器和判断器打分的标准是与环境信息的一致性,而不是客观事实,因此单纯追求达到纳什均衡,不一定能保证答案合理。
为了避免二者同时出错的情况出现,开发者还引入了正则化纠错机制。
首先是向生成器和判别器基于客观事实的先验策略,而不是任由其随机初始化。
这些先验策略是生成器和判别器生成策略的“金科玉律”,引导了策略的优化方向。

在此还有一种KL惩罚策略,当新的策略出现时,会计算其与初始策略的KL散度(又叫相对熵)。
KL散度描述了二者之间的相关性,数值越大,相关性越低。
假设P(x)和Q(x)分别是随机变量X上的两个概率分布,则在离散和连续的情形下,KL散度分别为:
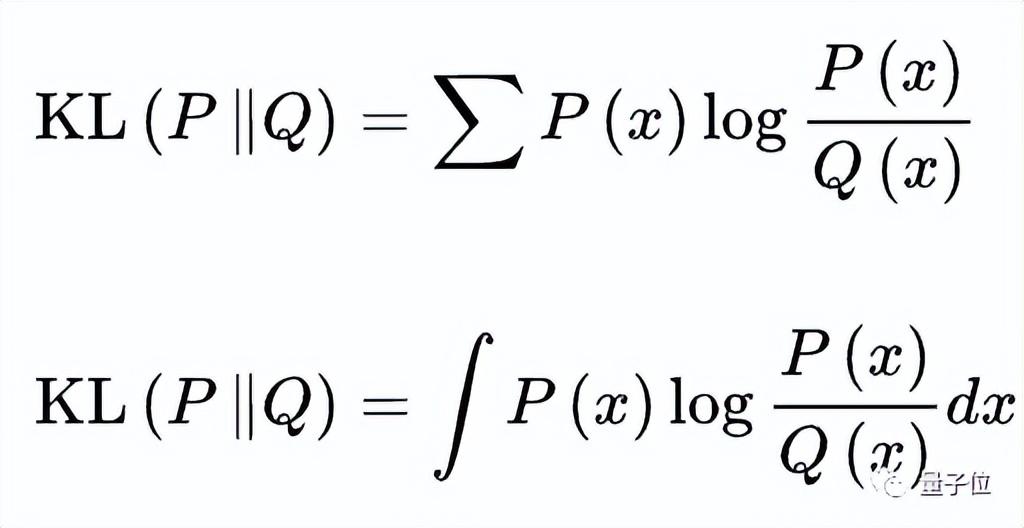
这一结果会加入到生成新策略的函数当中,避免了最终生成的结果偏离客观事实。
如下式所示,奖励函数U中包含了KL散度项,并设置了惩罚系数λ(>0)。
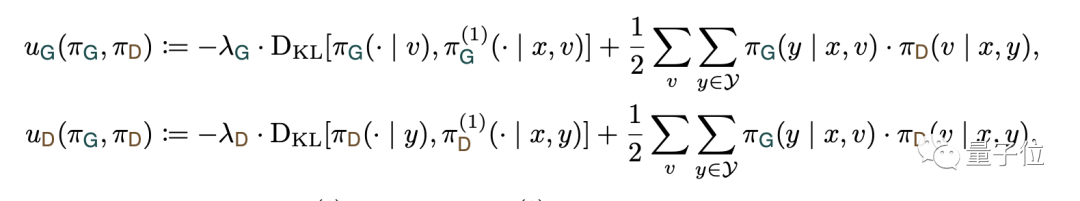
当KL散度越大,也就是和客观事实偏差越大时,模型获得的奖励分数将会降低。
这样一来,当生成器和判别器结果一致却不符合事实时,相关结果不会获得高评分,也就不会成为最终答案。
凭借着这样的策略,研究团队用更低的消耗让7B的Llama取得了优异的成绩。
部分能力超越“谷歌版GPT”
总的来说,均衡排序优化后的Llama在常识推理、阅读理解、数学和对话任务中的表现都十分出色。
选择题方面,同样是Llama,经均衡排名方法优化之后,模型在MMLU等多个数据集上的成绩都排在比较靠前的位置。
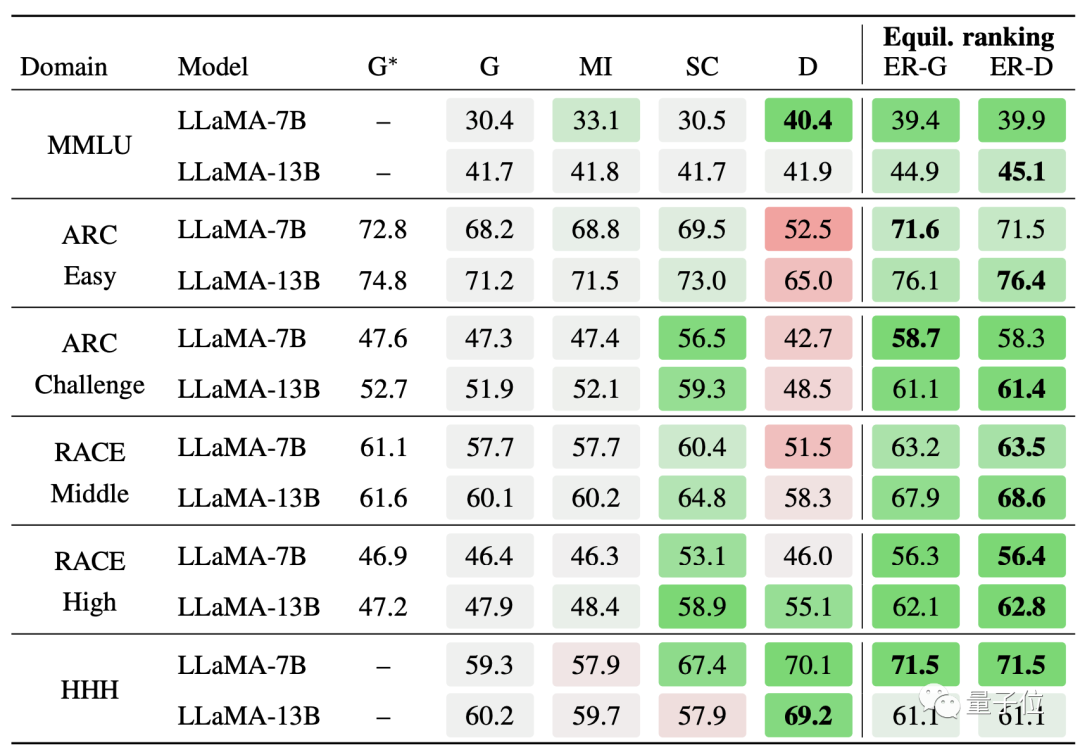
问答题方面,均衡排名策略优化后的13B Llama在TruthfulQA数据集中取得了最佳成绩,7B版本也与第一名相差无几。
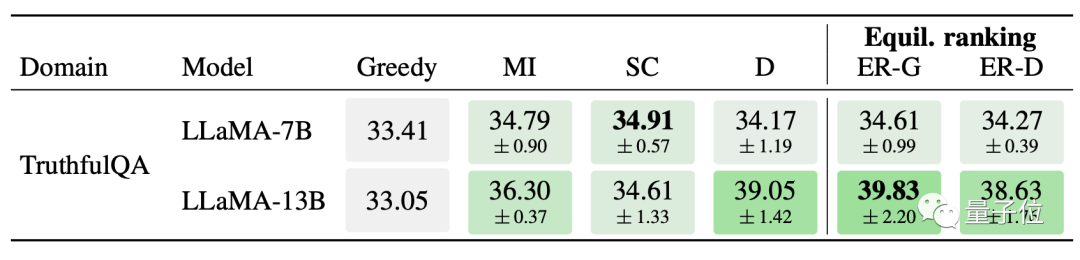
除了文本相关的理解和推理,模型在数学方面也达到了较高水平。
7B Llama模型的诸多优化方式中,均衡排序取得了GSM8K测试的最好成绩。
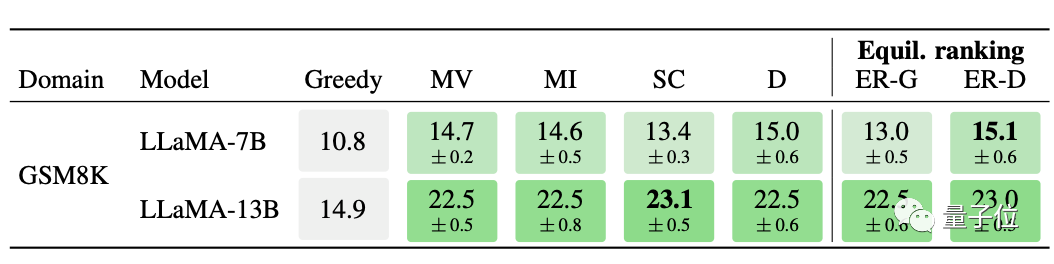
均衡排序方法不仅是诸多Llama优化方式中的佼佼者,优化后的Llama成绩也超过了其他模型。
在ARC数据集的Challenge分集和RACE数据集的High分集上,Llama-7B+均衡排序的准确率分别为58.3%和56.4%,显著超越了PaLM-540B的53.0%和49.1%。
更多具体细节,可以到原论文中一探究竟。
论文地址:
http://arxiv.org/abs/2310.09139
—完 —