原文链接:https://mp.weixin.qq.com/s/N2fj1Apyu6B2eqb-T1uAkg
李梅、施方圆 AI科技评论

作者 | 李梅、施方圆
编辑 | 陈彩娴
10 月 5 日,AlphaTensor 横空出世,DeepMind 宣布其解决了数学领域 50 年来一个悬而未决的数学算法问题,即矩阵乘法。AlphaTensor 成为首个用于为矩阵乘法等数学问题发现新颖、高效且可证明正确的算法的 AI 系统。论文《Discovering faster matrix multiplication algorithms with reinforcement learning》也登上了 Nature 封面。
然而,AlphaTensor 的记录仅保持了一周,便被人类数学家打破了。
来自奥地利林茨约翰·开普勒大学的研究人员 Manuel Kauers 和 Jakob Moosbauer 在其最新工作中表示,他们已经打破 AlphaTensor 的矩阵乘法记录。他们开发了一种以 95 步执行 5×5 矩阵乘法的方法,比 AlphaTensor 的 96 步记录少了一步,此前的记录为 98 步。论文预印版于 10 月 13 日发布在 arxiv 上。

论文地址:https://arxiv.org/abs/2210.04045
论文标题中的 “FBHHRBNRSSSHK”其实就是 DeepMind 论文所有作者姓氏的首字母组合,这种命名方式也是很有趣了:

数学问题的探索永无止境,如作者所说,DeepMind 算法方案 “still not the end of the story”。不过,他们这次的突破是站在巨人也就是 AI 的肩膀上,作者表示,其解决方案是在 DeepMind 方案的基础上应用一系列的转换,从而消除了一步乘法计算。
1
前进 2 步的 AlphaTensor
我们先来简要回顾一下 AlphaTensor 的成绩。
计算机科学中许多数学任务都是通过矩阵乘法来处理的,例如机器学习、计算机图形的创建,各种模拟或数据压缩。而计算机计算乘法的速度要远远慢于加法,因此,即使矩阵乘法的效率提升得很小,也会产生巨大影响,几十年来,数学家们一直在寻找更有效的矩阵乘法算法。
1969 年,德国数学家 Volker Strassen 开发了一种算法,首次将 4×4 矩阵乘法的求解从 64 步减少到 49 步,震动了数学界。
而 Deepmind 这次发布的 AI 系统 AlphaTensor,发现了一种比 Strassen 算法更快的新算法。Demis Hassabis 称,新算法具备在每天数万亿次计算中将效率提高 10% ~ 20% 的潜力。
AlphaTensor 是一次从游戏到数学的飞跃,它基于 2018 年 Deepmind 发布的通用棋盘游戏 AI 系统 AlphaZero。为了训练 AlphaTensor,Deepmind 研究团队将矩阵乘法问题转化成一种 3D 棋盘游戏,每一步都会产生新算法的构建块。AlphaTensor 每次会在数万次移动中进行选择,以尽可能少的步骤生成新算法而获得奖励。Deepmind 将其称为“张量游戏”。
在 5×5 的输入矩阵中,AlphaTensor 独立发现了 Strassen 算法和其他已知的算法。并且,它还开发了比旧算法更有效的新算法。
例如,5×5 矩阵乘法(n=4)以前要计算 80 步,而 AlphaTensor 新算法只需 76 步;当n=5 时,AlphaTensor 将求解从原来的 98 步减少到 96 步。4×4 矩阵乘法由 Strassen 减少到 49 步,AlphaTensor 则将其优化到 47 步。这样的效率是由 AlphaTensor 生成的 70 多个矩阵乘法的算法实现的。
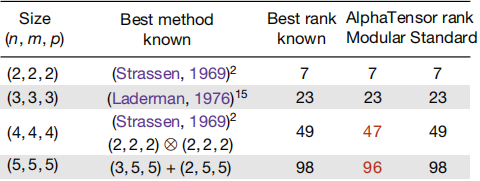

图注:AlphaTensor 发现的算法复杂性与已知矩阵乘法算法比较
此外,AlphaTensor 还可开发特定硬件的算法,用于机器学习。据说目前运行速度比谷歌 TPU 和英伟达 V100 上的算法快 20%。
自主调整乘法算法以适应硬件的方法对人类来说很困难,所以 AlphaTensor 对 Strassen 算法的改进创造了 4×4 矩阵乘法的新上限,是 AI 进步为其他学科提供助力的一大证明。它也表明,原本为传统游戏开发的 AlphaZero 系统可以解决领域之外的数学问题。
2
人类再向前 1 步
在 Manuel Kauers 和 Jakob Moosbauer 的最新研究中,他们主要有两个新发现,一是对于 4×4 矩阵,他们提出了另一种 47 步乘法的求解算法,但不同于先前的解决方案;二是对于 5×5 矩阵,他们首次提出了一种需要 95 步乘法的方案。
在这篇文章中,作者简单展示了这两个矩阵乘法的方案,不久后将发表正式论文,更详细地介绍求解算法的搜索技术。
4 × 4 矩阵的新方案共包含 47 次乘法,如下:
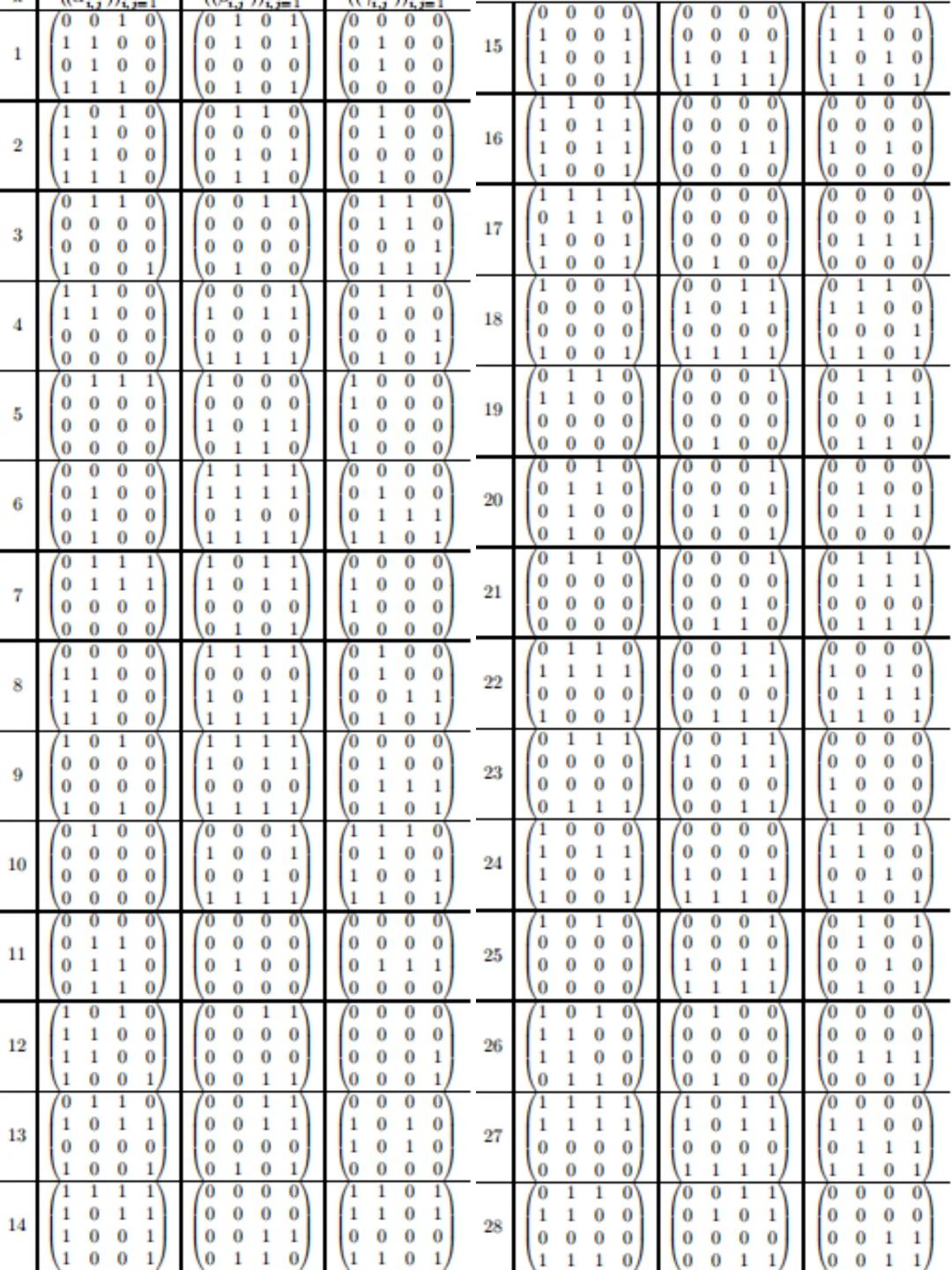
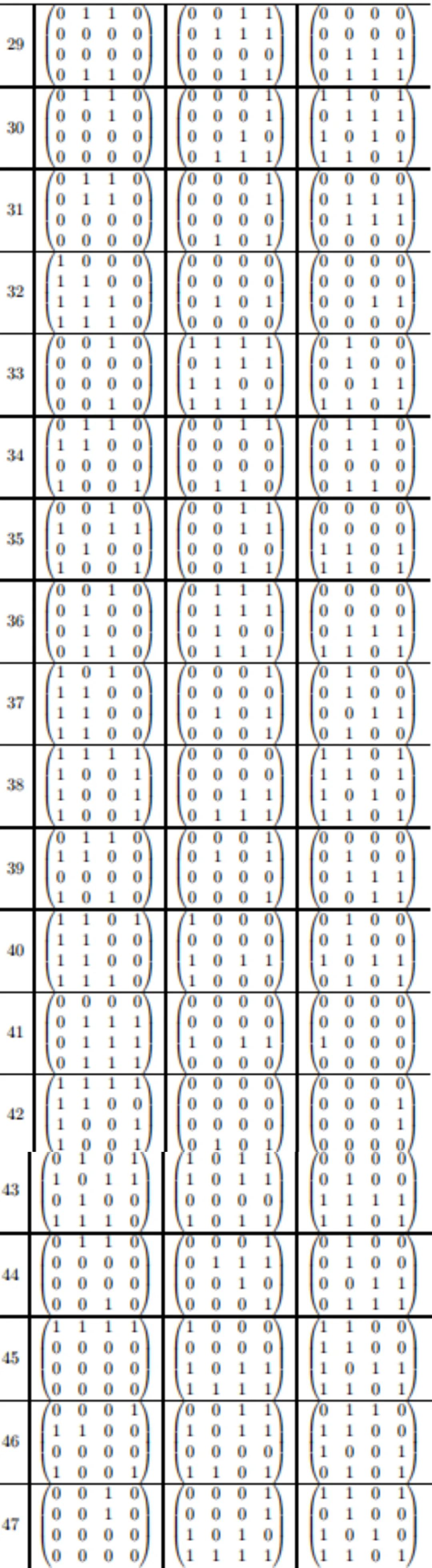
5×5 矩阵(n=5)的 95 步乘法方案如下:
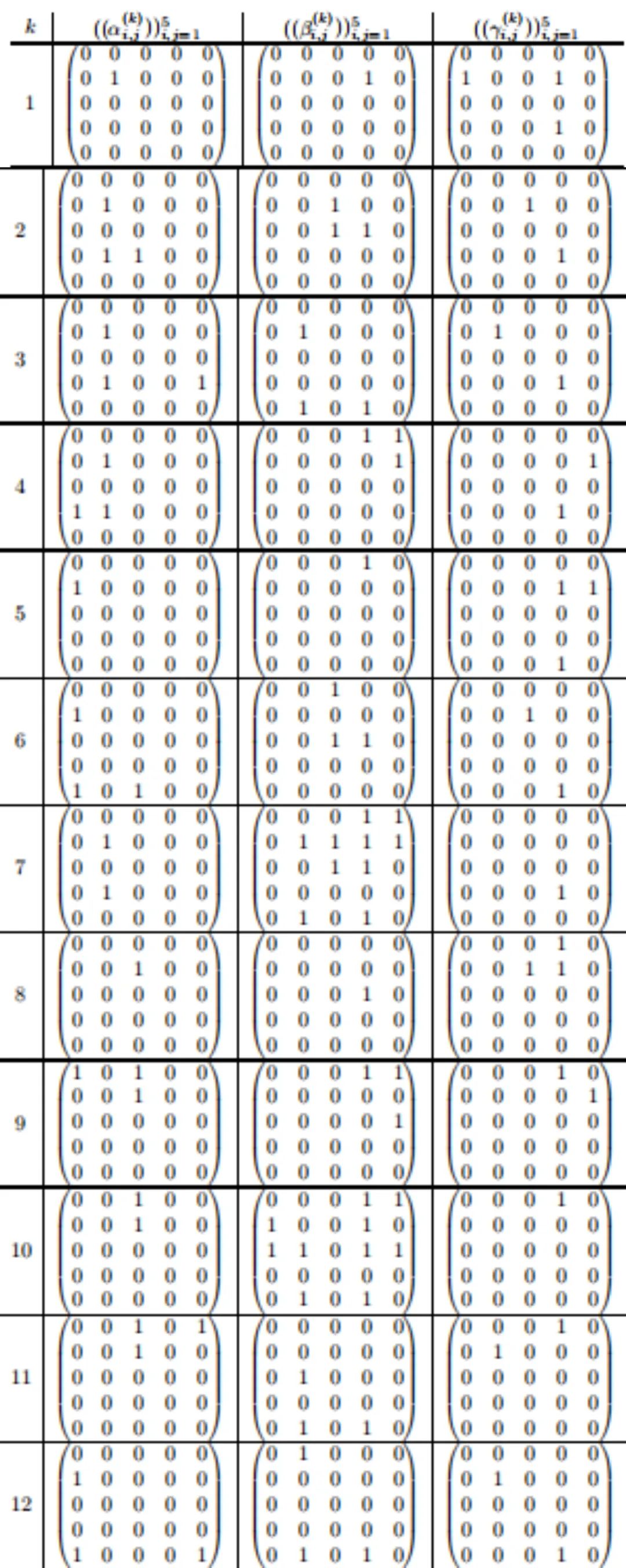

考虑到 GPU 每天要进行万亿次矩阵计算,所以从 98 步到 96 步以及从 96 步到 95 步这样看起来很小的增量改进,实际上能大大提升计算效率,可以让 AI 应用程序在现有硬件上运行得更快。
作者介绍:

Manuel Kauers,林茨约翰内斯开普勒大学的代数教授,该大学代数研究所的负责人。其研究兴趣是计算机代数、符号求和和积分、特殊函数恒等式等。

Jakob Moosbauer,林茨约翰内斯开普勒大学代数研究所博士生。
参考链接:
1.https://the-decoder.com/deepmind-alphatensor-record-for-matrix-multiplication-held-for-a-good-week/