原文链接:https://mp.weixin.qq.com/s/jrJRQ2gJJOyCrk8xMDAAEw
原创 十三维 集智俱乐部

导语
意识如河流般迁流不断,又能流转变异乃至瞬息万变。如何描述大脑中这些既具有鲁棒性又对输入信号极度敏感的认知过程与意识形成?最近发表在 Physics Reports 的新研究通过亚稳态和异宿网络建立了大脑信息过程的序列动力学,用一组以各种认知过程中可转移模式为解的非线性微分方程,解释了大脑的认知、意识和创造力过程。该工作有望推广向社会心智、机器人、人工智能和生物医学等领域研究。
三维 | 作者
郑木华 | 审校
邓一雪 | 编辑
大脑是一个复杂的动力学网络,全脑网络结构与相应的心理过程、局部特异化功能和全脑协调之间有着复杂的动态关系,用动力学方程给出大脑活动一个普适的描述一直是个棘手的问题。最近几位跨国协作的科学家在《Physics Reports》上发表的一篇论文《Sequential dynamics of complex networks in mind: Consciousness and creativity》中,通过引入亚稳态(metastable states)和耦合异宿网络(coupled heteroclinic networks)对大脑网络的动力过程的表示,建立了符合脑成像和实验观察的网络序列动力学模型,并解释了创造力的产生机理以及与意识、情感、注意力等各种认知活动之间的关系。

论文题目:
Sequential dynamics of complex networks in mind: Consciousness and creativity
论文地址:
https://www.sciencedirect.com/science/article/abs/pii/S0370157320302908
1. 亚稳态与异宿网络
很多实验研究表明,大脑使用离散的经济策略来表示、生成和处理认知信息。例如能够实现低维描述的分层循环脑网络分析,以定位与环境交互的自我意识动态[1,2] 。其中大脑的序列瞬态动力过程可以看作是可观察的亚稳态序列转换的结果[3-5]。亚稳态是一种物理和化学中的概念,它指比稳态(基态)的时间更短、比激发态时间更长的一种特殊的激发态,对动力系统而言,它包含很多非稳态情况的不变子集。

图1:亚稳态与稳态
一个动力系统会沿着稳定的流形在一定时间内充分接近亚稳态(以某种非稳态平衡或非稳态周期轨道),并沿着不稳定流形(Manifolds)离开[6]。在动力系统理论中,不同亚稳态之间的路径(相空间轨迹)被称为“异宿轨”(heteroclinic trajectories/orbits),其中异宿环(heteroclinic cycle)指的是连接平衡点、周期解或混沌不变集(如吸引子)之间解轨迹的集合,它通常以马鞍形状汇集连接。这些解轨迹集合的网络即异宿网络。相对的,相同亚稳态之间的路径被称为同宿轨(homoclinic orbits),在下图中可以看到它们之间的区别。
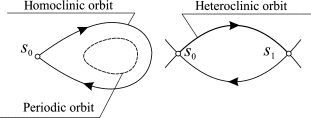
图2:同宿轨与异宿轨
作者认为,大脑要想有效地适应处理多种灵活的认知过程,就必须能够在瞬态模式下切换到特定的认知任务工作,因此这种状态就不能仅仅是一种平衡态或完全周期性振荡,在相应相空间中不能用稳定点、极限环或吸引子来有效表示。而异宿网络则因为会存在很长时间接近某种平衡态,然后迅速转变状态的间歇性行为性质,所以特别适合用来理解和描述神经动力系统。
如下图所示,A 表示静态信息项的的亚稳态序列,绿色和蓝色之间的 Sk(k=i,i+1,i+2,……) 为异宿轨的马鞍平衡点;B 表示动态亚稳态序列,在这种情况下代表异宿轨的就是马鞍形的周期性轨道。
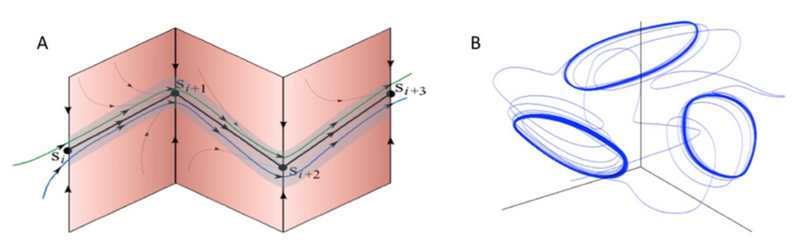
图3:能在相空间中实现鲁棒性瞬态动力过程的异宿轨
这样一来认知过程就可以描述为类似信息模式的操作,例如在空间模式集上,通过不同的亚稳态的多种切换序列模式来实现众多目标[3,7],其中各种可转移状态就代表了与认知编码相关的信息项目,如一种感知觉(视觉、听觉、嗅觉模式)、一个认知决策、一种记忆图示等。
论文研究的另一个基础是大脑全局心智活动中的无赢家竞争原则(Winnerless competition principle)。这个原则在许多不同的非线性耗散多主体系统(生态、社会、生理等)中都被观察到过,它意味着大脑会对功能网络的兴奋和抑制进行调度,并以此整合各种时空尺度的认知信息,可以解释诸如工作记忆局限、注意力集中转换、情感和认知之间的动态关系、言语产生等许多现象。
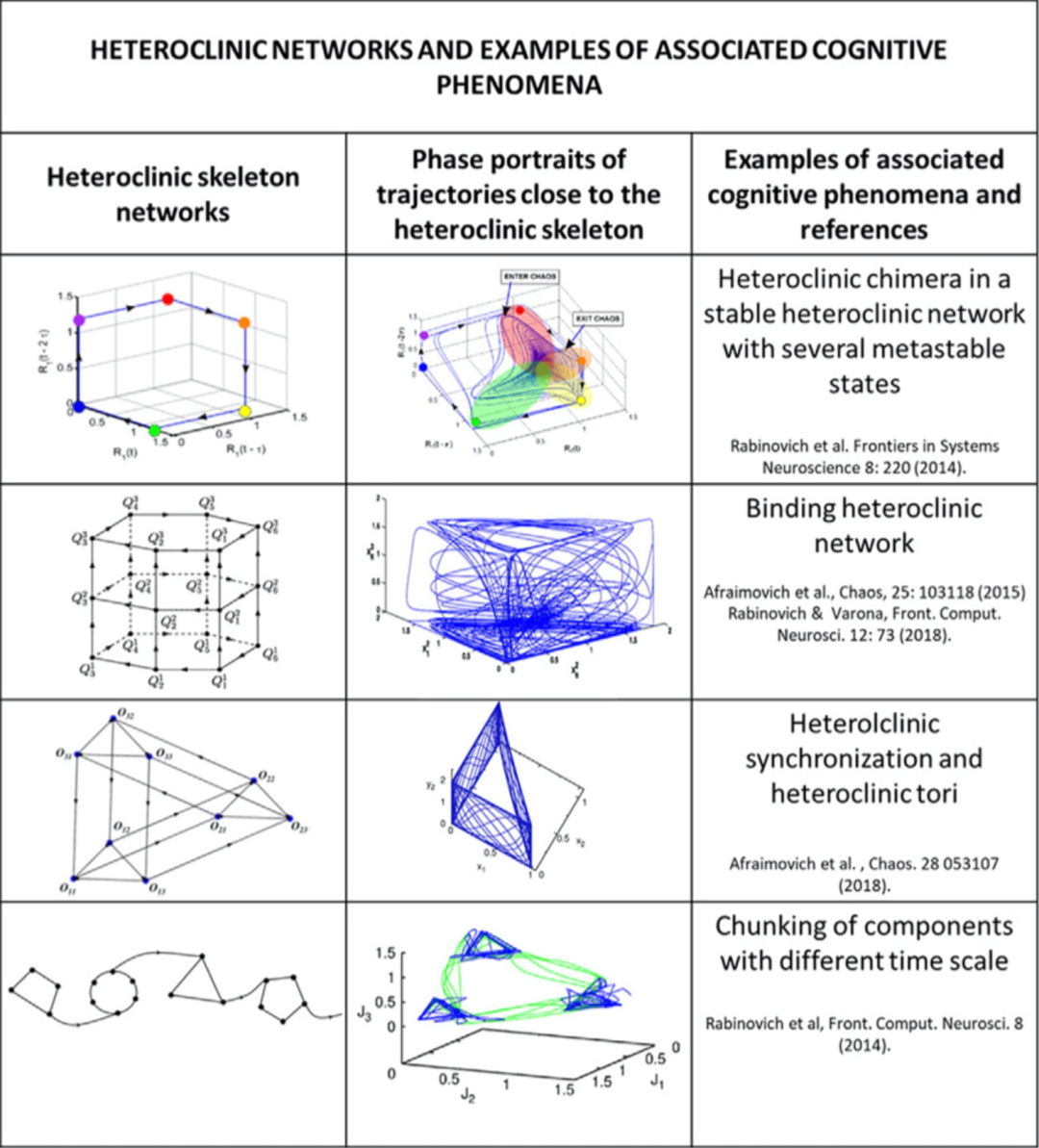
图4:异宿网络反映了大脑多层级尺度的认知现象
作者认为异宿网络的性质证实了著名心理学家威廉·詹姆斯关于意识的描述:大脑中的活动就像一个充满各种不连续事件的意识流,并据此满足以下约束条件给出了大脑认知活动描述的一组瞬态序列动力学方程:
1. 方程解对应认知过程的可转移模式
2. 满足无赢家竞争原则、具有瞬态切换的创造力和潜在鲁棒性
3. 作为开放的耗散系统,在抑制和激发之间保持总体平衡
4. 对记忆和环境信息敏感
图5:大脑的序列动力学模型和方程
2. 创造力的动力学
根据序列瞬态序列动力学,可以对大脑很多认知活动进行解释,例如创造的产生。创造的出现意味着产生了新的隐喻,这对应于大脑自我活动中信息变化在分叉时的突然改变,即动力系统在异宿轨上向某个混沌不变集激活了新的自由度。
创造的动力过程是三种认知模态相互作用的结果:
1. 默认网络(如头脑风暴和白日梦)
2. 自传体记忆的执行控制网络(当需要将注意力集中在某个目标时,该网络就会被激活)
3. 突显网络(Salience network):检测环境刺激,并在执行控制和默认网络之间切换注意力[8]。
如下图所示,注意力、记忆和情绪等认知资源基本模态之间的振荡抑制互动图式,由一系列分层的异宿网络构成。在序列动力学方程中这些模态用变量X0、X1、X2表示。圆圈边缘对应抑制性连接,圈内则是一些更低层的异宿网络,代表诸如一首诗的段落,一个爵士乐旋律的基本块,舞蹈编排中一个基本动作等信息模块。
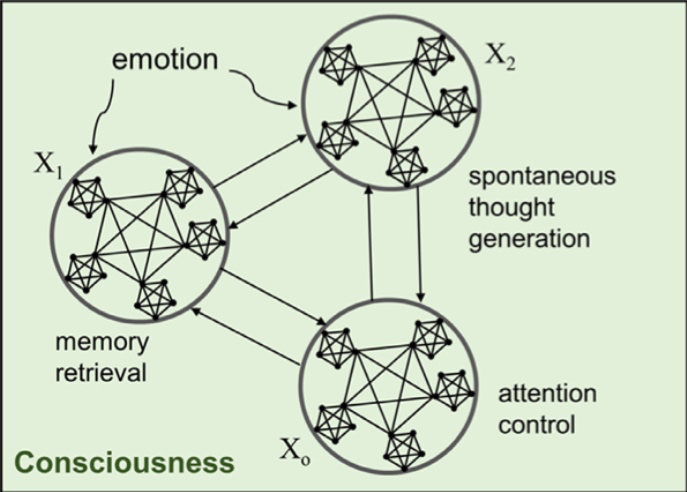
图6:注意力、记忆和情绪三种基本模态之间的互动创造过程
根据大脑的序列动力学方程,还会推导出两种不同的创造模式,如下图所示,一种持续时间无限长,可以作为音乐、诗歌等时间过程来回忆 (a,b) ,一种则是新出现的短暂的非常规序列信息,如波洛克的油画或偶发性的烹饪菜肴 (c,d)。
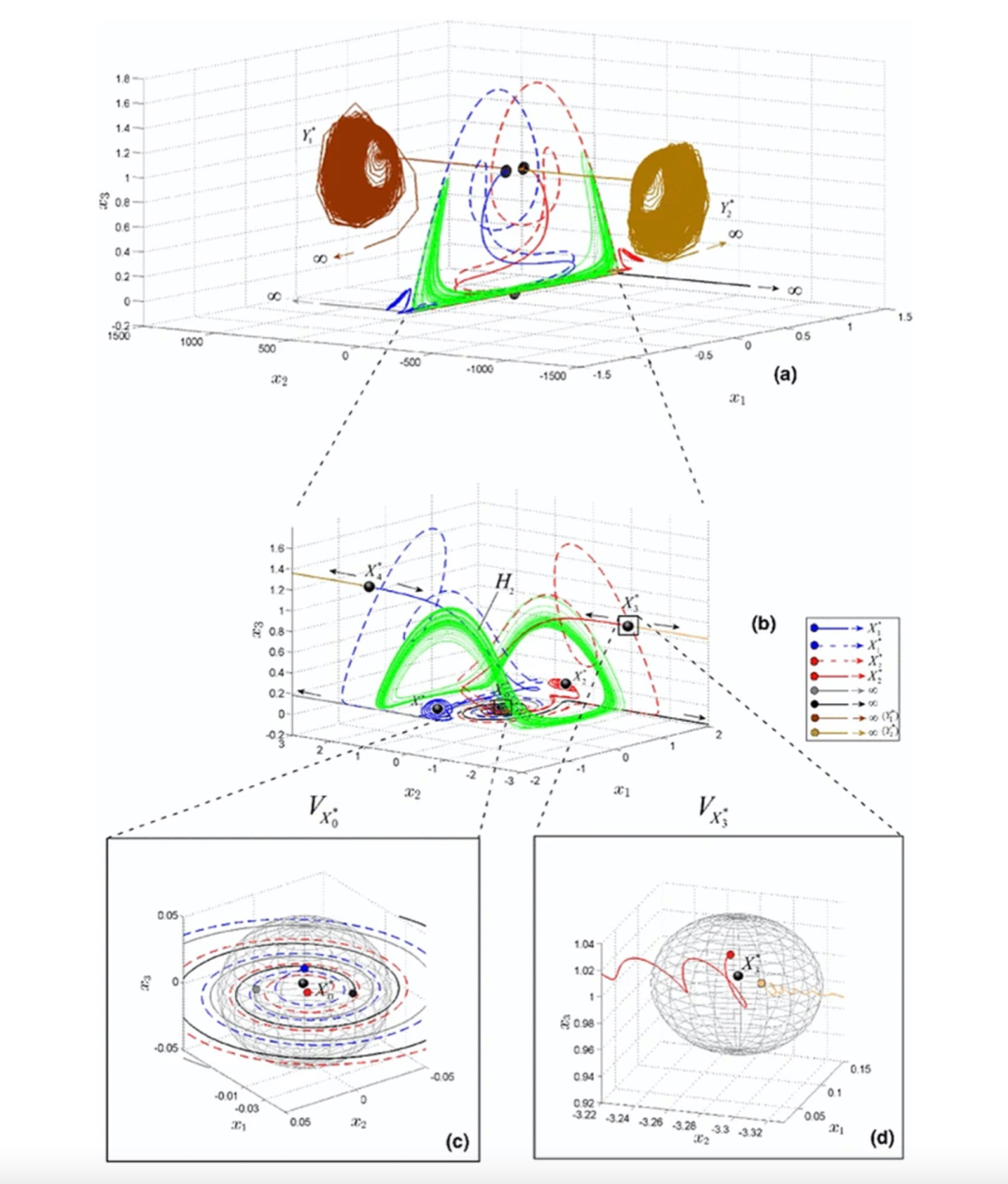
图7:(a,b) 轨迹划向无限的绿色隐藏吸引子);(c,d) 被吸引出现在稳定平衡附近的其它轨迹 [9]
3. 走向认知与意识的通用框架
作者认为,大脑的序列复杂网络动力学是一个通用的框架,可以解释很多大脑活动并应用到广泛的研究领域中。例如,意识同样可以被视为大脑中一个短暂的多模态时空过程,是许多特化功能在全脑网络整合活动的结果,动力学方程可以很好地描述意识活动的时序、多模态约束、同步或节律化等。这还包括情绪和注意力的产生,以及如何在社会群体中不同个体大脑之间进行迁移和协作等,这意味着这组动力学方程可以解释诸如集体心流(group flow)之类的现象。作者认为接下来分析研究社会群体中信息过程的时空结合动态会是一个很有前途的方向。
此外,还有对机器人、人工智能和生物医学方面的应用。无论是基于规则的决策系统,还是机器学习,异宿网络和无赢家竞争原则都可以广泛应用于具有认知交互的多智能体的系统中,反映各种内部和外部信息模态的表征和动力转换过程,使得其具有创造力、产生“机器意识”,甚至能为形成“人机统合心智”(human-robot mind)提供一种可能的协调控制机制。在生物医学方面则可据此发展出各种节律刺激性技术等。
总之这篇论文意义十分重大,十分需要和期待后续研究者在各个领域进行验证、补充、拓展和应用。
参考文献:[1] J.J. Gibson, The Ecological Approach to Visual Perception, Psychology Press, 2014.[2] R.W. Gibbs Jr., Embodiment and Cognitive Science, Cambridge University Press, 2005.[3] M.I. Rabinovich, R. Huerta, P. Varona, V.S. Afraimovich, Transient cognitive dynamics, metastability, and decision making, PLoS Comput. Biol. 4 (2008)e1000072, http://dx.doi.org/10.1371/journal.pcbi.1000072.[4] S.L. Bressler, J.A.S. Kelso, Cortical coordination dynamics and cognition, Trends Cogn. Sci. 5 (2001) 26–36, http://dx.doi.org/10.1016/S1364- 6613(00)01564-3.[5] E. Tognoli, J.A.S. Kelso, The metastable brain, Neuron 81 (2014) 35-48, http://dx.doi.org/10.1016/j.neuron.2013.12.022.[6] P. Ashwin, M. Timme, Nonlinear dynamics: when instability makes sense, Nature 436 (2005) 36–37, http://dx.doi.org/10.1038/436036.[7] M. Rabinovich, R. Huerta, G. Laurent, Transient dynamics for neural processing, Science 321 (2008) 48–50, http://dx.doi.org/10.1126/science. 1155564.[8] R.E. Beaty, Y.N. Kenett, A.P. Christensen, M.D. Rosenberg, M. Benedek, Q. Chen, A. Fink, J. Qiu, T.R. Kwapil, M.J. Kane, P.J. Silvia, Robust prediction of individual creative ability from brain functional connectivity, Proc. Natl. Acad. Sci. USA 115 (2018) 1087–1092, http://dx.doi.org/10.1073/ PNAS.1713532115.[9] M.-F. Danca, N. Kuznetsov, G. Chen, Unusual dynamics and hidden attractors of the Rabinovich–Fabrikant system, Nonlinear Dynam. 88 (2017) 791–805, http://dx.doi.org/10.1007/s11071-016-3276-1.