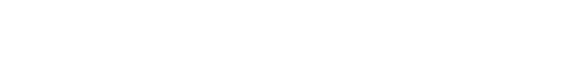原文链接:https://mp.weixin.qq.com/s/twK_0Mc2JwvPFPTewGauSQ
原创 Manfred Eppe等 集智俱乐部

导语
尽管人工智能技术突飞猛进,但截止目前,人类和动物在解决许多问题(尤其是复杂系统问题)的能力明显优于人工系统。理解人类等高等动物解决问题的能力,并在人工智能系统中模拟实现,是重要的科学命题。近日发表在Nature Machine Intelligence杂志的长文综述,概述了层次化问题解决的认知基础,以及如何利用强化学习技术实现抽象和预测能力,并提出小样本学习是关键。该综述能够指导启发未来应对复杂系统问题的机器学习架构设计。本文是对该综述的全文翻译。
研究领域:强化学习,多主体建模,认知复杂性,小样本学习,认知神经科学
Manfred Eppe等 | 作者
郭瑞东 | 译者
陈斯信 | 审校
邓一雪 | 编辑
论文题目:
Intelligent problem-solving as integrated hierarchical reinforcement learning
论文地址:
https://www.nature.com/articles/s42256-021-00433-9
1. 摘要
认知心理学和相关学科指出,生物智能体解决复杂问题的能力的发展,依赖于层级化的认知机制。层级化强化学习(hierarchical reinforcement learning)是一种很有前景的计算方法,最终可能会在人工智能和机器人身上产生类似的解决问题的能力。然而,至今为止,许多人类和非人类动物的解决问题的能力显然优于人工系统。在本文中,我们提出了将受生物启发的层级化认知机制整合起来的几个步骤,来赋予人工智能体先进的解决问题技能。我们首先回顾了认知心理学的文献,强调组合式抽象( compositional abstraction)和预测处理(predictive processing)的重要性。然后,我们将所获得的见解与当代的层级化强化学习方法联系起来。有趣的是,我们的研究结果表明,所识别的所有认知机制,都已经在不同的计算架构中分别实施过了。这便引出了一个问题:为什么没有一个统一的架构去集成它们?对该问题的回答是本文最后一个贡献。我们提供了一个新的综合的视角,来说明形成这样一个统一的结构,需要解决的计算性挑战。我们希望该综述能够引导受更复杂的认知结构启发的层级化机器学习架构。
人类和其它智慧动物,能够将复杂问题拆解为简单的、之前学过的子问题。这种层级化的方式,使他们能够一次解决之前没有遇到的问题,即,不需要任何试错。例如,图1描述了乌鸦是如何采用3个有因果连接的步骤,解决了一个复杂的食物获取难题的:它首先捡起一个棍子,用棍子获得石头,之后使用石头触发机关释放食物[1]。许多类似的实验,证明了灵长类动物、章鱼,当然还有人类的类似能力[2,3]。人类和动物认知研究指出,层级化的学习和解决问题的能力,对建立解决复杂问题的能力至关重要[2,4,5]。这带来了一个问题:我们如何能够让智能体和机器人,也具有类似的层级化学习和零样本问题解决(zero-shot problem-solving)的能力呢?

图1. 一只新喀里多尼亚乌鸦解决了一个获取食物的问题。a. 首先,这只乌鸦捡起一根棍子。b.c. 然后,它通过棍子从一个管道里拖出一块石头。d.e. 最后,它用石头来触发机关,获取食物。尽管乌鸦以前从未解决过这种问题,但在短暂的考察后,它立即能够解决这个问题。这样的零样本问题解决,是层级化的、有目标的计划的一个典型例子,它涉及到心理模拟,并依赖于适合任务的、组合式的抽象。作者的推测是,因为乌鸦一次只能看到立方体设置的一个侧面,它必须提前计划[1]。因此,乌鸦必须在心智上模拟未来的步骤。其中还涉及迁移学习:迁移并结合以前学到的类似子问题的解决方案,来解决新问题。成功的计划和转移学习只有在抽象的组合式的心理表征发展起来后才可能发生,例如,这些表征可以编码工具操作选项。然而,为了学习不同的工具操作,乌鸦依靠其内在动机,通过玩耍和试验工具来获得知识。图片由R. Gruber和A. Taylor提供[1]。
我们试图在强化学习的框架下,解决该问题[6-8]。多项研究表明,强化学习在生物上和认知上是可行的。很多现有的基于强化学习的方法,试图进行零样本问题解决和迁移学习[8,9],但目前,这只适用于与之前的任务相同或者相近的任务[10],或是在简单生成域中的任务[11,12],例如在二维的网格状世界中。类似图1中乌鸦的,在连续空间中的解决问题的行为,还没有在任何人工系统中实现。鉴于层级化强化学习所占比例较小,我们认为,对层级化学习和问题解决的关注是不够的。
在该综述中,我们通过三步来弥补上述的差距。首先,我们评估了层级化决策的神经认知基础,并识别出使高级问题解决能力得以实现的重要机制。之后,我们揭示了当前的层级强化学习方法的整合问题,指出大部分已被实现的生物学机制,都是以孤立而非整合的方式实现的。第三,我们指出整合关键方法和机制的步骤,以克服上述整合问题,发展一个统一的认知框架。
2. 神经认知基础
下文指出:生物体的复杂的问题解决技能,可以用几种特定的认知能力清晰描述,这些能力依赖于几项核心认知机制,包括抽象(abstraction),内在动机(intrinsic motivation)和心智模拟(mental simulation)。
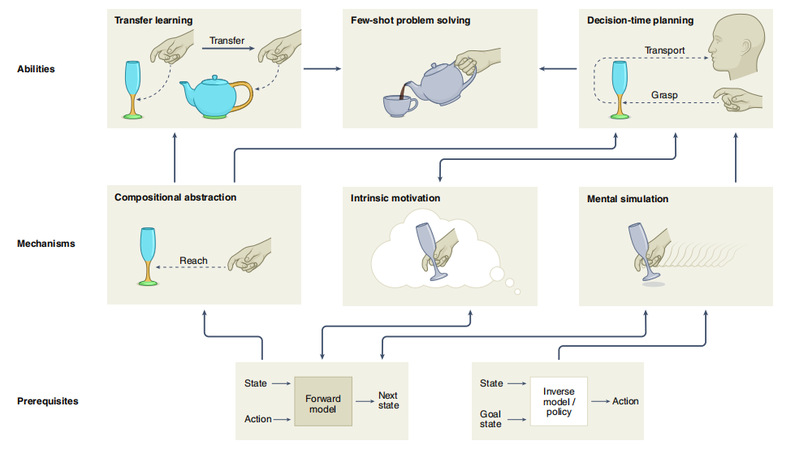
图2展示了这些机制如何在前向或逆向的模型(作为神经活动的先决条件)中发展出来。
2. 生物体解决问题的先决条件、机制和特征。前向和反向模型是高阶认知机制和能力的先决条件。组成式抽象,允许智能体将问题分解为可复用的子结构,例如,学习到物体的哪一部分是易于抓取的,比如玻璃杯的杯颈。在前向模型的帮助下,内在动机可以驱动智能体,以一种搜索信息的、认知的方式与环境互动。例如,内在动机引导智能体与杯子互动,来了解杯子特征。心智模拟使得探索可能的状态-行为顺序成为可能,例如,想象伸向玻璃杯的手的位置将如何演变。在上述机制的帮助下,智能体能够经由层级化的、组合式的目标驱动规划,灵活地达到想要的状态,例如,喝水的规划是先正确地抓取杯子,再妥当地移动杯子。组合式抽象使得智能体能够进行迁移学习,例如,像抓取其它有柄的物体(如茶壶)一样,去适当地抓取杯杯颈,从而使小样本问题解决成为可能。
3. 认知能力
我们关注认知能力的以下特征和性质:
小样本问题解决(Few-shot problem-solving):小样本问题解决,指在少于5次的尝试下,解决未知问题的能力。而零样本问题解决,是小样本问题解决的一种特殊情况,指不需要额外尝试即可解决新问题。例如,在之前解决过相关问题,但没有经过进一步训练的情况下,乌鸦可以使用木棍作为工具,解决全新的食物获取问题(图1)。我们指出,要这样解决问题,有两种能力至关重要:迁移学习(transfer learning)和决策时规划(decision-time planning)。
迁移学习:迁移学习允许生物体将之前任务的解法,迁移到一个新的但相似的任务上,从而使小样本的问题解决成为可能。这显著地减少了,有时甚至消除了解决一个新问题所需要尝试的次数。
这样的类比推理,通常被认为是人类认知的关键性基石。例如,认知学理论指出,人类是通过类比其它领域的知识,来理解机械系统的[13]。除此之外,教育理论指出,人类在明确地接受识别不同问题间相似性的训练后,迁移学习能力会提高[14]。然而,尽管人类能够熟练地用类比来解决问题,要发现新的类比,却好像很困难。这便是功能固化(functional fixedness)的现象:人类在解决问题时,倾向于以习以为常的方法去使用物体[15]。
目标导向的规划(goal-directed planning)。行为传统上分为两类,刺激驱动的习惯性行为,以及目标导向的,规划好的行为[16-18]。习惯性行为指高度自动化的,计算高效的,主要从之前的强化过程中学到的应激性控制[17]。对该方式的一种批判来自Tolman[19,20],他指出,大鼠在迷宫中探索一次后,能够更快地找到食物,即使最初的探索行为没有带来奖励。这一结果指出,大鼠对迷宫构建了一个表征(representation)或认知地图(cognitive map),使得它们能够在奖励(reward)出现时,规划它们的行为。在理解目标导向的规划方面,人工智能和认知科学的进展相互影响。对于动作控制,一个有影响力的模型是TOTE(test–operate–test–exit,测试-动作-测试-离开)[21],其中,动作是基于一个迭代的、层级化的反馈循环进行选择的。在这里,想要的的预期状态与当前的感觉状态进行比较,来选择下一个动作。类似TOTE,很多最新的理论,都将规划看作一种层级化的过程,涉及不同层级的抽象[5,22,23]。
但规划过程考虑了什么样的信息呢?动作生成的观念运动(Ideomotor)理论指出,预期动作的效果决定了动作的选择。与此相对应,事件编码(event encoding)理论[25]指出,一个动作的表征和它们的效果存储在共享的编码中,对动作-效果的预期,可以直接激活相关动作的编码。上述动作产生和效果预测之间的联系,还受到了一系列实验证据的支持[25-27]。
4. 迁移学习和规划的认知机制
前文讨论了迁移学习和规划能力是如何让智能体具有小样本问题解决能力的。但是什么使迁移学习和规划能力成为可能的?我们的调研指出,迁移学习和规划所需的三种认知机制是感觉运动抽象(sensorimotor abstraction),内在动机(intrinsic motivation)和心智模拟(mental simulation)。
感知运动的抽象。根据具身认知(embodied cognition)理论,抽象的心智概念,可以从基于身体的,感觉运动的,与环境的互动经验中推出[2,28-30]。这里,我们区分动作抽象(action abstraction)和状态抽象(state abstraction)。动作抽象指对一串在时间上延展的原始动作、选项或运动基元的抽象[32,33]。例如,运输一个物体,就是动作抽象,因为它包含了一连串更基本的动作,例如伸手去够物体和抬起物体(图3)。
状态抽象指对(部分)环境的精简编码,其中不相关的细节被去除。由此,状态抽象会将一个场景分出和任务相关的部分,例如可抓性,容器性或空心度。例如,酒杯和茶杯都是容器,也都是可以抓取的(图3)。同时,容器意味着它是中空的,这说明这种抽象有层级化和组合式(compositional)的特征。认知语言学和相关研究表明,抽象能力受益于组合性(compositionality)[34]。正式地说,如果一个表述,是由其子表述,和决定子表述组合语义的规则所组成,我们就称该表述具有组合性。思维语言假说(the language of thought theory)[35]将来自语言的组合性原理,用到抽象的心智表征上,声称思想也具有组合性。例如,人类可以从语言描述中,将他们已知的成分进行组合,轻易地想象之前没有见过的影像[36],即使是通过很奇怪的描述——想想一条骑着滑板的粉红色的龙会是什么样子。
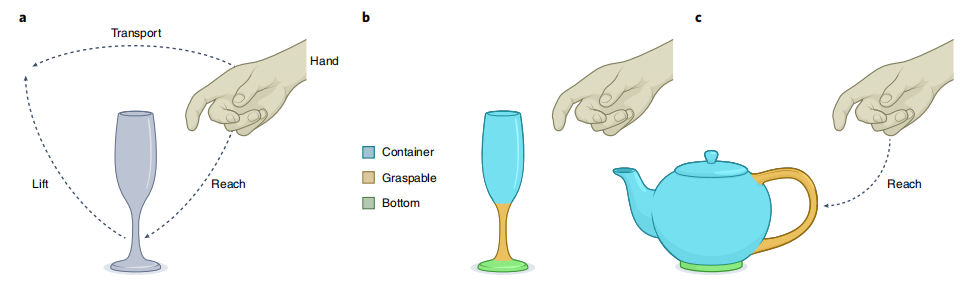
图3. 组合式的动作抽象与状态抽象。a. 动作抽象描述了一连串原始动作。b. 状态抽象编码了状态空间的特定性质。c. 抽象的组合性,使得它们能够通过将抽象的定义(伸手可抓取的目标)实例化(instantiate)为具体的物体(茶壶),来被通用地应用。
对抽象心智表征进行编码,是由局部符号,还是分布式地,还存在争议[37],但在这两种情况下,都有证据表明存在组合可泛化能力。例如,Haynes[38]指出,位于腹外侧前额叶皮层的神经编码,记录着复合行为的规则,可以被分解为编码各自组成部分的神经编码。
对于感觉动作抽象(sensorimotor abstractions),组合规则(rules of composition)需要由我们的心智灵活推断,从而根据我们的世界知识,形成合理的环境配置[29,39,40]。这种常识组合性,使抽象能够以有意义的方式应用。对一个抽象成分(例如抓取的目标)的填入被限制在使用的对象上(例如,可抓取的物体,如茶壶),如图3。从算法视角来看。常识组合性有巨大的计算优势:抽象,例如对抓取行为的编码,如果能够使用于多种场景(例如不同的抓取目标),会更加经济。常识组合性,通过在表征间建立映射,本质上简化了对类比的识别,这一优势在关于创造力的概念整合(concept blending)的认知理论中,也广为人知[41,42]。
内在动机。通过设立内在动机的目标,内在动机影响着目标导向的归因。从认知发展的角度来看,内在动机这个术语,是用来描述‘搜索新事物……探索,学习的内在倾向’的[43]。这里的内在,和外在价值相对,指的不是满足需求或者规避不想见到的结果。内在动机引出了一般的探索行为,好奇心和嬉戏。好奇心指以收集信息为目标的探索行为[45-47]。好奇心和嬉戏密切相关,后者是以提高技能为导向的新奇互动。在多种智慧动物中,都可以观察到嬉戏行为,例如狗和乌鸦[48]。
心智模拟。心智模拟,指的是智能体能够在多种表征层面,预测环境动态的能力。例如,人们认为,动作想象使得运动员能够通过在内心模拟这个运动动作,来改进对高难度身体动作(例如倒翻转)的执行[49],工程师在开发机械系统时,也依赖心智模拟[13]。多项研究指出,心智模拟在更高级的推理过程中,也发挥作用,例如,[50-52]报告了心智模拟是如何在因果概念层面,改善对未来行为的规划的。
作为功能前提的前向和反向模型
感觉动作抽象,内在动机和心智模拟,都是需要一个合适神经功能基础的复杂机制。我们提出,这一关键基础可以由前向和反向模型构成[24]。前向模型预测一个动作如何影响世界,而反向模型决定要实行一个目标所需要执行的动作。
心智模拟的前向和反向模型。为了进行心智模拟,一个智能体需要一个前向模型,来模拟环境是如何演化的(可能取决于智能体的动作)。然而,对所有可能动作的可能结果进行预测,很快变成计算上不可行的。因此,动作选择要求建立,从当前状态和想要的内在心智状态,到可能动作的,更直接的连接。这可通过行为策略的反向模型实现,该模型生成完成当前目标的可能动作。
内在动机的前向和反向模型。内在动机也需要正向和反向模型。例如,对内在的前向学习过程模型,被证明是将好奇心建模为一种内在奖励的有效方式[47,53,54]。Friston等人指出,当使用前向模型进行主动推断时,会涌现出内在驱动的行为[44,45],这意味着,推断动作的过程最小化了预期自由能。作者认为,主动推断会导致认知探索,在这个过程中,智能体采取不同的行为,以减少其前向预测的不确定性[45,46]。然而,主动推断(active inference)和自由能原理(free energy principle),都被批判为过于宽泛,而且可证伪性存疑[57]。
抽象和奠基的前向和反向模型。多种认知理论,包括预测性编码(predictive coding)[58],自由能原理[59]和贝叶斯大脑假说(Bayesian brain hypothesis)[60],都将大脑看成一种生成机制,会持续地试图匹配输入的感官信号和对它们的概率预测[61]。在这一框架下,在多个处理层级上,预测交互式地双向进行:自上而下的信息,为预测感官信号提供了额外的信息;而自下而上的错误信息,被用来修正高层级的预测[62]。Butz[29]提出,这样的层级化处理涌现出了抽象的、组合式的、更高层级的编码,例如“容器”的概念,这使得对低层特征的预测(例如该容器所包含的物体的封闭和运输)成为可能。时间分隔理论(Event segmentation theory)[63],使得前向预测在学习感觉运动抽象过程中的作用更为明显。根据这一理论,瞬时性的预测误差,被用来将连续的体验流分割为概念事件编码。
5. 计算实现
层级化强化学习的一系列机制在计算机中的实现(如图4)并不像在生物体中整合得那么好。下文将概述当前最先进的,与神经认知基础相关的计算实现方式。
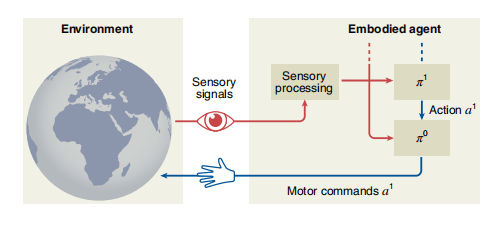
图4. 通用的层级化问题解决架构。每一个层级的抽象,都分别有独立的策略πi。大部分现有的层级化强化学习关注两个层级,高层级的动作是一个动作a1基元或子目标,而低层级的动作a0是直接影响环境的运动指令。
迁移学习和少样本规划能力
我们对神经认知基础的调研指出,迁移学习和规划,是小样本问题解决的两项基础认知能力。但我们如何在计算上对它们进行建模呢?
迁移学习。迁移学习对于层级化架构来说是很自然的,因为该架构可以复用高层级的通用技能,将它们用在不同的低层级任务上,反之亦然。因此,在当前迁移学习中,有很大比例的方法是建立在复用低层级策略上的[64-72]。研究者不仅考虑了在不同任务间的,也考虑了在不同机器人,即不同形态的智能体之间的迁移学习[65,73,74]。
规划。规划可分为决策时规划和后台规划(background planning)[8,75]。决策时规划指搜索一系列动作,来决定为达成特定目标,接下来要采取什么动作。搜索是通过用特定领域的动力学的内部预测模型模拟动作来实现的。决策时规划,使零样本问题解决成为可能,因为智能体只在内部预测模型指出动作能达成预期目标时,才会执行规划的动作。后台规划,是Sutton[76]提出的一种基于模型的强化学习方法。它使用前向模型模拟动作,来训练得到特定策略。这可以提高采样效率,但还不足以使小样本的问题解决成为可能。
在传统的人工智能中,层级化的决策时规划是一个广为人知的范式[77],但将它和层级化的强化学习结合的方法却很罕见。有些方法会通过基于动作规划的高层级的决策,和基于强化学习的低层级的动作控制,将动作规划和强化学习结合[10,70,78,79]。这些方法证明,决策时规划对于离散状态-动作空间中的高层级推断格外有用。
迁移学习和规划背后的机制
我们对迁移学习和规划背后认知原理的总结,揭示了生物智能体的学习和问题解决能力的三个重要的认知机制:感觉运动的组合式抽象(compositional sensorimotor abstraction),内在动机和心智模拟。
感觉动作的组合抽象及奠基。层级化强化学习,具有时序和表征两个维度,还能区分动作和状态的抽象。对动作的时序抽象,将复杂的问题分解为层级化的简单问题。影响力最大的表征动作抽象方法,是基于行为基元[65,68,70,80-84]构建的(图5a),其中包括了选择、次级策略和原子化的高层级技能。这些行为基元位于一个抽象的表征空间中,例如,在一个充满动作标签和索引的离散有限空间中。而较为新进的高层级动作表征,则是由低层级的状态空间中的子目标所构成[10,74,85-90](图5b)。在这里,智能体通过完成一系列子目标,来实现最后的目标。
图5. 不同类型的动作抽象。a. 基于动作基元,智能体通过选择一系列高层级的动作,而不具体指定每一个动作会导致的中间状态,来决定达到最终状态的路径。b. 存在子目标时,智能体指定要达成最终状态的子目标,而不指定达成子目标的动作。
当前很多基于视觉输入的强化学习方式,都使用卷积神经网络来提供一个相对通用的抽象,其中所有层级都使用同一个抽象的视觉特征图[11,12,67,91-94]。该策略的问题是它忽略了“不同层级的推断需要不同层级的抽象”这一事实:例如,对于运输任务,物体的具体形状和重量,只与低层级的运动控制有关。更高层级的规划层,只需要抽象事实,诸如某个物体是否是可抓的或可运输的。因此,表征状态的抽象,应该和其要使用的层级相一致。我们将这样的抽象称为适合推断的抽象。当前的强化学习方法,对解决该问题已有不小样本,但大多基于手动定义的抽象函数[10,79,82,95]。也有一些特例,其状态抽象是自动从层级化强化学习中导出的,例如通过聚类[85,96],经由特征表征[97]或通过因子化(factorization)[98]。
认知科学还指出,组合性是抽象表征的一个重要特征。例如,一个符号化的组合式的动作表征抓(杯子),允许在“抓取”这一动作和“杯子”这一物体间进行调控。对于分布式数值化的表征,例如向量,组合性也是适用的。例如,如果v1可以由其它向量,例如v2和v3,组合而成,而且存在一个以解释组合规则的向量操作,例如v1=v2·v3,那么可以说这个向量v1具有组合性。
认知科学中,有充足的证据表明,组合性可以改善迁移学习[98]。考虑到迁移学习的确依赖问题之间的相似性,这些证据从计算角度来说是有道理的。其它由认知科学启发的计算方法,例如概念整合(concept binding)[41],进一步证明了,较少的可能类比映射提高了可迁移性。此外,Jiang等人的研究工作[67]提供了实证数据,指出具有组合式的表征能提升学习的迁移能力。他们使用自然语言,这一内在组合式表征,来描述层级话强化学习中的高层级动作,并表明,自然语言的表征,相比非组合式的表征,提升了迁移学习的效果。
内在动机。使强化学习具有稳定性的一个有效方法,是采用内在动机,即,在稀疏的外在的奖励之外,增加与领域无关的内在奖励。有内在动机的层级化强化学习最常见的方法是:在子任务/目标完成时提供内在奖励[10,11,69,78,82,99-103]。
其它提供内在动机的方式,包括识别一组具有多样性[64,99,104]或可预测性[70]的基本行为,以及识别适合于重组高层任务的基元。
另一种在非层级的强化学习中常见的内在奖励模型,是基于惊讶度(surprise)和好奇心[47,54,105,106]。在这些方法中,惊讶度通常被建模为前向预测误差的一个函数,而好奇心则是通过,在智能体遇到惊讶度时提供内在的奖励,来实现的。然而,在层级化的设定下,只有[89,99,107]采用了惊讶度,证明了好奇心能显著提升学习的性能。层级化的好奇心可能可以带来协同(synergy),因为一个有好奇心的高抽象层级,会自动地为低层级生成学习任务。例如,它会产生难度适中的子任务,供低层级去完成。困难之处在于找到难度恰好的条件,并找到探索(explorative)和利用(exploitative)这两个子任务之间的适当平衡。
心智模拟。心智模拟使智能体能够预测自身以及他者动作的影响。因此,这是使智能体具有事先规划能力的一项关键机制。心智模拟的计算实现方式包括基于模型的强化学习[76],动作规划[77]以及两者的综合[10,108]。尽管有认知科学的证据表明心智模拟发生在多个表征层面[2,36],层级化的心智模拟方法却是很少的。只有少数整合了强化学习规划的层级化方法是建立在心智模拟上的[10,70,78,79,103,109],不过,这些模型也仅在较高规划层应用了心智模拟。Wu等人的工作[110]是一个例外,它在低层级使用了心智模拟,决定哪些子策略将被执行。另一个例外是[111],它在多个任务层都使用了心智模拟来进行规划。然而,我们还不知道有什么方式是进行了层级化的后台规划的,即,通过在多层执行的动作,来训练一个层级化的策略。高层级的后台规划缺失的一个可能的理由是,它需要稳定的低层级的表征,而对相应的稳定标准的建模是很难的。
感觉运动抽象:内在动机和心智模拟的先决条件
基于策略或反向模型的强化学习,会预测一个在当前状态下,能够最大化奖励或完成特定目标的动作。与之相对的,前向模型会根据当前状态,和要采取的一系列动作,预测未来的状态。文献调研指出,大部分层级化强化学习,在高层级和低层级,都使用了反向模型。而有的方法只在低层级使用反向模型[10,70,78,79,103,109],在高层级决策时则使用决策时规划。文献综述还指出,有数项机制对于迁移学习,规划和小样本问题解决,是必要的,或至少是能有利的,而这些机制需要前向模型。有一些非层级的强化学习,使用了前向模型进行感觉运动抽象[105,112]。这是通过自监督的方式达成的:前向预测是在一个潜在的抽象空间中学习的。但目前,这一机制,还没有用层级化的方式采用过。
对于采用好奇心作为内在动机的模型,前向模型也是有用的,例如,对智能体在惊讶出现时给与奖励,其中惊讶度是预测误差的函数[55]。好奇心已被证明,能缓解强化学习中的稀疏奖励问题[89,105]。但除了[89,107]等少许例外,很少有使用层级化前向模型,来产生层级化好奇心的尝试。
6. 讨论和展望
当前的层级化强化学习策略,有如下缺点。这些缺点是由融合不同机制过程中的特定挑战产生的(图6)。在此,我们通过具体的算法建议来解决这些缺点。
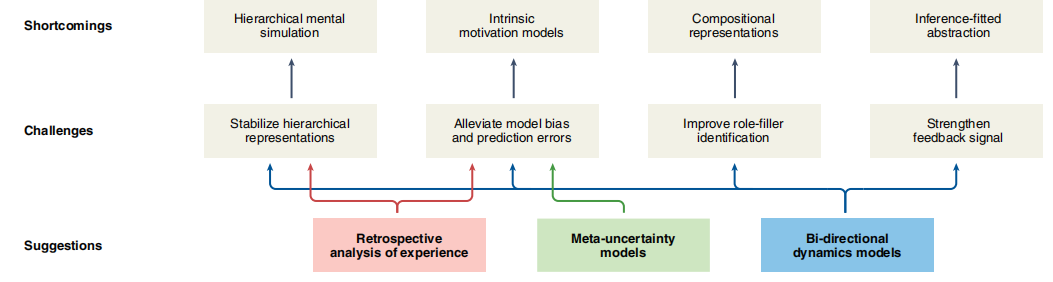
图6. 层级化强化学习的缺陷,挑战和建议。计算实现部分概述了当代层级化强化学习方法的几个缺点。我们认为,这些缺点至少来自四个核心挑战,并就有助于解决这些挑战的关键方法提出了三点建议。
层级化强化学习架构的缺点和挑战
以下各节指出了当前方法的主要挑战。
层级化的心智模拟,需要稳定的层级表征和精确的预测。大部分当前的小样本解决问题,都依赖迁移学习,但它们既没有利用决策时的规划,也没有考虑后台规划来发挥层级化心智模拟的好处。尽管很多非层级化的方法指出,心智模拟可以提升采样效率[113,114],但仅有一项研究在多层级上使用了层级化的心智模拟[111]。这一缺失的主要原因,是高层级的前向模型在开始训练时,低层级的策略应该已经收敛。该问题在无模型的强化学习中已被解决[64],但对于预测性的前向模型,还没有相关研究。
内在动机需要模型具有精确的不确定性应对能力。在50篇调研的文献中,只有9篇应用了多样性和好奇心,这个比例是偏低的。神经认知基础一节介绍了大量的认知证据,表明这些机制对生物智能体的智能行为至关重要[56]。
这一缺陷的一个潜在原因,是基于预测的内在动机模型,受到了当前前向计算模型中,对不确定性过于简单的处理的影响,这是带噪声的观察或混沌不可预测的动态系统要面对的问题。例如,通过最大化前向模型的预测误差,Roder等人[89]实现了一种好奇心驱动的内在动机。但这会导致智能体遇到所谓的“不清晰的电视问题”,即智能体总是试图遇到不确定的观察(例如电视总是显示白噪音)。这会干扰学到层级化表征的问题,因为如果对这些表征的学习还没有收敛,就无法应对高层级表征的不确定性。
组合性要求精准的角色填充(role-filler)表征。只有少数的层级化强化学习研究考虑了组合性,例如使用自然语言,对动作进行表征[67],或基于符号逻辑进行组合式表征[11]。由于组成式表征通常建立在变值表征的基础上,因此,要缓解这一缺陷,需要首先在更基础的层面上对这些表征进行研究。图神经网络(graph neural networks),一种对实体和其间的关系通过一个图中的节点(node)和连边(edge)编码的神经网络模型,是实现组合式表征的可行方式。当提供了背后的图结构后,图神经网络能够更好地泛化,并支持关系推理[115]。然而,从数据中发现一个合适的抽象图,仍然是一个开放问题。
适配推断的状态抽象需要强学习信号。最近的层级化强化学习方式[86,89],对层级中的每一层,使用相同的状态表征,然而,在认知科学上,更可行的是让不同的抽象层级,有该层级推断所需要的抽象水平。例如,高层级的推断,只需要知道物体是否能够被抓取,而不必考虑物体的具体形状。对于低层级的推断,这样的细节信息是必须的。有的强化学习方法,通过卷积自编码器,从视觉数据中学习状态抽象[114]。然而这样的表征,是为了重现输入的视觉特征最优化的,而不是为决策最优化的。此外,在近期基于视觉的架构[11,12,67,91-94]中,强化学习智能体所有的层级,都接收相同的图像嵌入。因此,这里的抽象并不是为推断适配的。学习得到适配推断信号的问题在于:与其它方法如监督学习相比,强化学习的奖励信号对学习过程的推动作用相对较弱。
7. 展望和对上述挑战的建议
在下文中,我们概述了计算性关键方法如何有助于解决上述挑战。
对体验的回溯式分析。层级化强化学习的一个核心问题,是只有在低层的学习过程已收敛之后,高层的表征才会出现[64]。我们想指出,对体验的回顾式分析,可以缓解该问题。通过后见(hindsight)来训练强化学习中的策略[86,116],即将一个策略执行后达到的世界状态,当成是想要的目标状态,已经证明了上述论点。我们指出,后见学习(hindsight learning)是更为一般的对与经验的回溯式分析的特殊形式。例如,可以在事后也学习层级化的前向模型,而不需要高级别层等待低级别层的收敛。我们设想,将还没有完全训练好的低层,在过去错误动作的结果,重新看作想要的结果,能够稳定高层级的表征。这一技术能够消除模型的偏差。
元不确定模型(Meta-uncentainty model)。在认知模拟和内在动机中,预测误差发挥了关键作用。在关于神经认知基础的章节,我们探讨了自由能原理,其中包含了两个基于预测处理模型的看似矛盾的机制。在一方面,是主动推断[117],试图最小化长期的惊讶度。这通过最小化前向模型的预测误差实现。另一方面,还有主动学习,它寻求信息增益的最大化。这可以通过不同的内在奖励函数,使不确定性[118]或预测误差[89]最大化来实现。Schwartenbeck等人[117],通过建立预期的不确定性[119],来解决这一矛盾,统一两种机制。这样,预期的和非预期的不确定性,就可以通过对不确定性的元分析来应对。我们提议,对高的元不确定性进行内在奖励,能够带来探索行为,带来短期较高但长期可预期较低的元不确定性。此外,新获得的对前向模型不确定性的确定性,能够带来更准确的,能够知晓自身局限的预测过程[120]。
双向动力学模型。双向动力学模型包括了前向及后向推断的模型。我们认为,这样的组合,有利于层级化架构中的表征抽象。这一猜想是基于Pathak等人[105]和Hafner等人[112]的工作的。他们结合前向和反向模型,通过自监督学习,来产生隐藏表征的研究。。双向模型在一个潜在的空间上运行,由一个抽象函数生成。通过在隐藏层上,同时进行前向和后向的预测,抽象函数具有了两个重要的特征。一,潜空间具有降噪能力,因为只有潜观察的可预测部分决定了前向和后向预测。二,由于模型是自监督的,因此提供了一个比相对较弱的奖励信号更稳定的反馈信号。这缓解了预测误差,并加强了整体的学习信号。
8. 总结
该综述对层级化问题解决的认知基础,及如何在当前的层级化强化学习中实现这些机制,进行了汇总。我们将小样本的问题解决,看成是智能体的终极目标,即智能体在尽可能少的尝试次数下,学会因果性地解决有意义的问题。作为我们的的核心研究问题,我们呼吁那些计算上的先决条件和机制,使人工智能体的问题解决能力能达到智能动物的水平。我们还指出结合不同机制时遇到的挑战。
我们意识到,我们总结的认知科学理论,通常是有争议且矛盾的(在神经认知基础一章)。然而我们的讨论指出,特定理论的组合,能够产生算法上的协同作用。换句话说,我们推断,特定的机制如果对某一计算架构有利,那么它对生物的神经系统也有利,反之亦然。这样认知科学和人工智能可相互启发,汇集成对两个领域都有意义的间接,助益人工智能与人类的未来。
参考文献
Gruber, R. et al. New Caledonian crows use mental representations to solve metatool problems. Curr. Biol. 29, 686–692 (2019).
Butz, M. V. & Kutter, E. F. How the Mind Comes into Being (Oxford Univ. Press, 2017).
Perkins, D. N. & Salomon, G. in International Encyclopedia of Education (eds. Husen T. & Postelwhite T. N.) 6452–6457 (Pergamon Press, 1992).
Botvinick, M. M., Niv, Y. & Barto, A. C. Hierarchically organized behavior and its neural foundations: a reinforcement learning perspective. Cognition 113, 262–280 (2009).
Tomov, M. S., Yagati, S., Kumar, A., Yang, W. & Gershman, S. J. Discovery of hierarchical representations for efficient planning.PLoS Comput. Biol. 16, e1007594 (2020).
Arulkumaran, K., Deisenroth, M. P., Brundage, M. & Bharath, A. A. Deep reinforcement learning: a brief survey. IEEE Signal Process. Mag. 34, 26–38 (2017).
Li, Y. Deep reinforcement learning: an overview. Preprint at https://arxiv.org/abs/1701.07274 (2018).
Sutton, R. S. & Barto, A. G. Reinforcement Learning: An Introduction 2nd edn (MIT Press, 2018).
Neftci, E. O. & Averbeck, B. B. Reinforcement learning in artificial and biological systems. Nat. Mach. Intell. 1, 133–143 (2019).
Eppe, M., Nguyen, P. D. H. & Wermter, S. From semantics to execution: integrating action planning with reinforcement learning for robotic causal problem-solving. Front. Robot. AI 6, 123 (2019).
Oh, J., Singh, S., Lee, H. & Kohli, P. Zero-shot task generalization with multi-task deep reinforcement learning. In Proc. 34th International Conference on Machine Learning (ICML) (eds. Precup, D. & Teh, Y. W.) 2661–2670 (PMLR, 2017).
Sohn, S., Oh, J. & Lee, H. Hierarchical reinforcement learning for zero-shot generalization with subtask dependencies. In Proc. 32nd International Conference on Neural Information Processing Systems (NeurIPS) (eds Bengio S. et al.) Vol. 31, 7156–7166 (ACM, 2018).
Hegarty, M. Mechanical reasoning by mental simulation. Trends Cogn. Sci. 8, 280–285 (2004).
Klauer, K. J. Teaching for analogical transfer as a means of improving problem-solving, thinking and learning. Instruct. Sci. 18, 179–192 (1989).
Duncker, K. & Lees, L. S. On problem-solving. Psychol. Monographs 58, No.5 (whole No. 270), 85–101 https://doi.org/10.1037/h0093599 (1945).
Dayan, P. Goal-directed control and its antipodes. Neural Netw. 22, 213–219 (2009).
Dolan, R. J. & Dayan, P. Goals and habits in the brain. Neuron 80, 312–325 (2013).
O’Doherty, J. P., Cockburn, J. & Pauli, W. M. Learning, reward, and decision making. Annu. Rev. Psychol. 68, 73–100 (2017).
Tolman, E. C. & Honzik, C. H. Introduction and removal of reward, and maze performance in rats. Univ. California Publ. Psychol. 4, 257–275 (1930).
Butz, M. V. & Hoffmann, J. Anticipations control behavior: animal behavior in an anticipatory learning classifier system. Adaptive Behav. 10, 75–96 (2002).
Miller, G. A., Galanter, E. & Pribram, K. H. Plans and the Structure of Behavior (Holt, Rinehart & Winston, 1960).
Botvinick, M. & Weinstein, A. Model-based hierarchical reinforcement learning and human action control. Philos. Trans. R. Soc. B Biol. Sci. 369, 20130480 (2014).
Wiener, J. M. & Mallot, H. A. ’Fine-to-coarse’ route planning and navigation in regionalized environments. Spatial Cogn. Comput. 3, 331–358 (2003).
Stock, A. & Stock, C. A short history of ideo-motor action. Psychol. Res. 68, 176–188 (2004).
Hommel, B., Müsseler, J., Aschersleben, G. & Prinz, W. The theory of event coding (TEC): a framework for perception and action planning. Behav. Brain Sci. 24, 849–878 (2001).
Hoffmann, J. in Anticipatory Behavior in Adaptive Learning Systems: Foundations, Theories and Systems (eds Butz, M. V. et al.) 44–65 (Springer, 2003).
Kunde, W., Elsner, K. & Kiesel, A. No anticipation-no action: the role of anticipation in action and perception. Cogn. Process. 8, 71–78 (2007).
Barsalou, L. W. Grounded cognition. Annu. Rev. Psychol. 59, 617–645 (2008).
Butz, M. V. Toward a unified sub-symbolic computational theory of cognition. Front. Psychol. 7, 925 (2016).
Pulvermüller, F. Brain embodiment of syntax and grammar: discrete combinatorial mechanisms spelt out in neuronal circuits. Brain Lang. 112, 167–179 (2010).
Sutton, R. S., Precup, D. & Singh, S. Between MDPs and semi-MDPs: a framework for temporal abstraction in reinforcement learning. Artif. Intell. 112, 181–211 (1999).
Flash, T. & Hochner, B. Motor primitives in vertebrates and invertebrates. Curr. Opin. Neurobiol. 15, 660–666 (2005).
Schaal, S. in Adaptive Motion of Animals and Machines (eds. Kimura, H. et al.) 261–280 (Springer, 2006).
Feldman, J., Dodge, E. & Bryant, J. in The Oxford Handbook of Linguistic Analysis (eds Heine, B. & Narrog, H.) 111–138 (Oxford Univ. Press, 2009).
Fodor, J. A. Language, thought and compositionality. Mind Lang. 16, 1–15 (2001).
Frankland, S. M. & Greene, J. D. Concepts and compositionality: in search of the brain’s language of thought. Annu. Rev. Psychol. 71, 273–303 (2020).
Hummel, J. E. Getting symbols out of a neural architecture. Connection Sci. 23, 109–118 (2011).
Haynes, J. D., Wisniewski, D., Gorgen, K., Momennejad, I. & Reverberi, C. FMRI decoding of intentions: compositionality, hierarchy and prospective memory. In Proc. 3rd International Winter Conference on Brain-Computer Interface (BCI), 1-3 (IEEE, 2015).
Gärdenfors, P. The Geometry of Meaning: Semantics Based on Conceptual Spaces (MIT Press, 2014).
Lakoff, G. & Johnson, M. Philosophy in the Flesh (Basic Books, 1999).
Eppe, M. et al. A computational framework for concept blending. Artif. Intell. 256, 105–129 (2018).
Turner, M. The Origin of Ideas (Oxford Univ. Press, 2014).
Deci, E. L. & Ryan, R. M. Self-determination theory and the facilitation of intrinsic motivation. Am. Psychol. 55, 68–78 (2000).
Friston, K. et al. Active inference and epistemic value. Cogn. Neurosci. 6, 187–214 (2015).
Berlyne, D. E. Curiosity and exploration. Science 153, 25–33 (1966).
Loewenstein, G. The psychology of curiosity: a review and reinterpretation. Psychol. Bull. 116, 75–98 (1994).
Oudeyer, P.-Y., Kaplan, F. & Hafner, V. V. Intrinsic motivation systems for autonomous mental development. In IEEE Transactions on Evolutionary Computation (eds. Coello, C. A. C. et al.) Vol. 11, 265–286 (IEEE, 2007).
Pisula, W. Play and exploration in animals—a comparative analysis. Polish Psychol. Bull. 39, 104–107 (2008).
Jeannerod, M. Mental imagery in the motor context. Neuropsychologia 33, 1419–1432 (1995).
Kahnemann, D. & Tversky, A. in Judgement under Uncertainty: Heuristics and Biases (eds Kahneman, D. et al.) Ch. 14, 201–208 (Cambridge Univ. Press, 1982).
Wells, G. L. & Gavanski, I. Mental simulation of causality. J. Personal. Social Psychol. 56, 161–169 (1989).
Taylor, S. E., Pham, L. B., Rivkin, I. D. & Armor, D. A. Harnessing the imagination: mental simulation, self-regulation and coping. Am. Psychol. 53, 429–439 (1998).
Kaplan, F. & Oudeyer, P.-Y. in Embodied Artificial Intelligence, Lecture Notes in Computer Science Vol. 3139 (eds Iida, F. et al.) 259–270 (Springer, 2004).
Schmidhuber, J. Formal theory of creativity, fun, and intrinsic motivation. IEEE Trans. Auton. Mental Dev. 2, 230–247 (2010).
Friston, K., Mattout, J. & Kilner, J. Action understanding and active inference. Biol. Cybern. 104, 137–160 (2011).
Oudeyer, P.-Y. Computational theories of curiosity-driven learning. In The New Science of Curiosity (ed. Goren Gordon), 43-72 (Nova Science Publishers, 2018); https://arxiv.org/abs/1802.10546
Colombo, M. & Wright, C. First principles in the life sciences: the free-energy principle, organicism and mechanism. Synthese 198, 3463–3488 (2021).
Huang, Y. & Rao, R. P. Predictive coding. WIREs Cogn. Sci. 2, 580–593 (2011).
Friston, K. The free-energy principle: a unified brain theory? Nat. Rev. Neurosci. 11, 127–138 (2010).
Knill, D. C. & Pouget, A. The Bayesian brain: the role of uncertainty in neural coding and computation. Trends Neurosci. 27, 712–719 (2004).
Clark, A. Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behav. Brain Sci. 36, 181–204 (2013).
Clark, A. Surfing Uncertainty: Prediction, Action and the Embodied Mind (Oxford Univ. Press, 2016).
Zacks, J. M., Speer, N. K., Swallow, K. M., Braver, T. S. & Reyonolds, J. R. Event perception: a mind/brain perspective. Psychol. Bull. 133, 273–293 (2007).
Eysenbach, B., Ibarz, J., Gupta, A. & Levine, S. Diversity is all you need: learning skills without a reward function. In International Conference on Learning Representations (ICLR, 2019).
Frans, K., Ho, J., Chen, X., Abbeel, P. & Schulman, J. Meta learning shared hierarchies. In Proc. International Conference on Learning Representations https://openreview.net/pdf?id=SyX0IeWAW (ICLR, 2018).
Heess, N. et al. Learning and transfer of modulated locomotor controllers. Preprint at https://arxiv.org/abs/1610.05182 (2016).
Jiang, Y., Gu, S., Murphy, K. & Finn, C. Language as an abstraction for hierarchical deep reinforcement learning. In Neural Information Processing Systems (NeurIPS) (eds. Wallach, H. et al.) 9414–9426 (ACM, 2019).
Li, A. C., Florensa, C., Clavera, I. & Abbeel, P. Sub-policy adaptation for hierarchical reinforcement learning. In Proc. International Conference on Learning Representations https://openreview.net/forum?id=ByeWogStDS (ICLR, 2020).
Qureshi, A. H. et al. Composing task-agnostic policies with deep reinforcement learning. In Proc. International Conference on Learning Representations https://openreview.net/forum?id=H1ezFREtwH (ICLR, 2020).
Sharma, A., Gu, S., Levine, S., Kumar, V. & Hausman, K. Dynamics-aware unsupervised discovery of skills. In Proc. International Conference on Learning Representations https://openreview.net/forum?id=HJgLZR4KvH (ICLR, 2020).
Tessler, C., Givony, S., Zahavy, T., Mankowitz, D. J. & Mannor, S. A deep hierarchical approach to lifelong learning in minecraft. In Proc. 31st AAAI Conference on Artificial Intelligence 1553–1561 (AAAI, 2017).
Vezhnevets, A. et al. Strategic attentive writer for learning macro-actions. In Neural Information Processing Systems (NIPS) (eds. Lee, D. et al.) 3494–3502 (NIPS, 2016).
Devin, C., Gupta, A., Darrell, T., Abbeel, P. & Levine, S. Learning modular neural network policies for multi-task and multi-robot transfer. In Proc. International Conference on Robotics and Automation (ICRA) (eds. Okamura, A. et al.) 2169–2176 (IEEE, 2017).
Hejna, D. J., Abbeel, P. & Pinto, L. Hierarchically decoupled morphological transfer. In Proc. International Conference on Machine Learning (ICML) (eds. Daumé III, H. & Singh, A.) 11409–11420 (PMLR, 2020).
Hamrick, J. B. et al. On the role of planning in model-based deep reinforcement learning. In Proc. International Conference on Learning Representations https://openreview.net/pdf?id=IrM64DGB21 (ICLR, 2021).
Sutton, R. S. Integrated architectures for learning, planning, and reacting based on approximating dynamic programming. In Proc. 7th International Conference on Machine Learning (ICML) (eds. Porter, B. W. & Mooney, R. J.) 216–224 (Morgan Kaufmann, 1990).
Nau, D. et al. SHOP2: an HTN planning system. J. Artif. Intell. Res. 20, 379–404 (2003).
MATH Lyu, D., Yang, F., Liu, B. & Gustafson, S. SDRL: interpretable and data-efficient deep reinforcement learning leveraging symbolic planning. In Proc. AAAI Conference on Artificial Intelligence Vol. 33, 2970–2977 (AAAI, 2019).
Ma, A., Ouimet, M. & Cortés, J. Hierarchical reinforcement learning via dynamic subspace search for multi-agent planning. Auton. Robot. 44, 485–503 (2020).
Bacon, P.-L., Harb, J. & Precup, D. The option-critic architecture. In Proc. 31st AAAI Conference on Artificial Intelligence 1726–1734 (AAAI, 2017).
Dietterich, T. G. State abstraction in MAXQ hierarchical reinforcement learning. In Advances in Neural Information Processing Systems (NIPS) (eds. Solla, S. et al.) Vol. 12, 994–1000 (NIPS, 1999).
Kulkarni, T. D., Narasimhan, K. R., Saeedi, A. & Tenenbaum, J. B. Hierarchical deep reinforcement learning: integrating temporal abstraction and intrinsic motivation. In Neural Information Processing Systems (NIPS) (eds. Lee, D. et al.) 3675–3683 (NIPS, 2016).
Shankar, T., Pinto, L., Tulsiani, S. & Gupta, A. Discovering motor programs by recomposing demonstrations. In Proc. International Conference on Learning Representations https://openreview.net/attachment?id=rkgHY0NYwr&name=original_pdf (ICLR, 2020).
Vezhnevets, A. S., Wu, Y. T., Eckstein, M., Leblond, R. & Leibo, J. Z. Options as responses: grounding behavioural hierarchies in multi-agent reinforcement learning. In Proc. International Conference on Machine Learning (ICML) (eds. Daumé III, H. & Singh, A.) 9733–9742 (PMLR, 2020).
Ghazanfari, B., Afghah, F. & Taylor, M. E. Sequential association rule mining for autonomously extracting hierarchical task structures in reinforcement learning. IEEE Access 8, 11782–11799 (2020).
Levy, A., Konidaris, G., Platt, R. & Saenko, K. Learning multi-level hierarchies with hindsight. In Proc. International Conference on Learning Representations https://openreview.net/pdf?id=ryzECoAcY7 (ICLR, 2019).
Nachum, O., Gu, S., Lee, H. & Levine, S. Data-efficient hierarchical reinforcement learning. In Proc. 32nd International Conference on Neural Information Processing Systems (NIPS) (eds. Bengio, S. et al.) 3307–3317 (NIPS, 2018).
Rafati, J. & Noelle, D. C. Learning representations in model-free hierarchical reinforcement learning. In Proc. 33rd AAAI Conference on Artificial Intelligence 10009–10010 (AAAI, 2019).
Röder, F., Eppe, M., Nguyen, P. D. H. & Wermter, S. Curious hierarchical actor-critic reinforcement learning. In Proc. International Conference on Artificial Neural Networks (ICANN) (eds. Farkaš, I. et al.) 408–419 (Springer, 2020).
Zhang, T., Guo, S., Tan, T., Hu, X. & Chen, F. Generating adjacency-constrained subgoals in hierarchical reinforcement learning. In Neural Information Processing Systems (NIPS) (eds. Larochelle, H. et al.) 21579-21590 (NIPS, 2020).
Lample, G. & Chaplot, D. S. Playing FPS games with deep reinforcement learning. In Proc. 31st AAAI Conference on Artificial Intelligence 2140–2146 (AAAI, 2017).
Vezhnevets, A. S. et al. FeUdal networks for hierarchical reinforcement learning. In Proc. 34th International Conference on Machine Learning (ICML) (eds. Precup, D. & Teh, Y. W.) Vol. 70, 3540–3549 (PMLR, 2017).
Wulfmeier, M. et al. Compositional Transfer in Hierarchical Reinforcement Learning. In Robotics: Science and System XVI (RSS) (eds. Toussaint M. et al.) (Robotics: Science and Systems Foundation, 2020); https://arxiv.org/abs/1906.11228
Yang, Z., Merrick, K., Jin, L. & Abbass, H. A. Hierarchical deep reinforcement learning for continuous action control. IEEE Trans. Neural Netw. Learn. Syst. 29, 5174–5184 (2018).
Toussaint, M., Allen, K. R., Smith, K. A. & Tenenbaum, J. B. Differentiable physics and stable modes for tool-use and manipulation planning. In Proc. Robotics: Science and Systems XIV (RSS) (eds. Kress-Gazit, H. et al.) https://ipvs.informatik.uni-stuttgart.de/mlr/papers/18-toussaint-RSS.pdf (Robotics: Science and Systems Foundation, 2018).
Akrour, R., Veiga, F., Peters, J. & Neumann, G. Regularizing reinforcement learning with state abstraction. In Proc. IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) 534–539 (IEEE, 2018).
Schaul, T. & Ring, M. Better generalization with forecasts. In Proc. 23rd International Joint Conference on Artificial Intelligence (IJCAI) (ed. Rossi, F.) 1656–1662 (AAAI, 2013).
Colas, C., Akakzia, A., Oudeyer, P.-Y., Chetouani, M. & Sigaud, O. Language-conditioned goal generation: a new approach to language grounding for RL. Preprint at https://arxiv.org/abs/2006.07043 (2020).
Blaes, S., Pogancic, M. V., Zhu, J. J. & Martius, G. Control what you can: intrinsically motivated task-planning agent. Neural Inf. Process. Syst. 32, 12541–12552 (2019).
Haarnoja, T., Hartikainen, K., Abbeel, P. & Levine, S. Latent space policies for hierarchical reinforcement learning. In Proc. International Conference on Machine Learning (ICML) (eds. Dy, J. & Krause, A.) Vol. 4, 2965–2975 (PMLR, 2018).
Rasmussen, D., Voelker, A. & Eliasmith, C. A neural model of hierarchical reinforcement learning. PLoS ONE 12, e0180234 (2017).
Riedmiller, M. et al. Learning by playing—solving sparse reward tasks from scratch. In Proc. International Conference on Machine Learning (ICML) (eds. Dy, J. & Krause, A.) Vol. 10, 6910–6919 (PMLR, 2018).
Yang, F., Lyu, D., Liu, B. & Gustafson, S. PEORL: integrating symbolic planning and hierarchical reinforcement learning for robust decision-making. In Proc. 27th International Joint Conference on Artificial Intelligence (IJCAI) (ed. Lang, J.) 4860–4866 (IJCAI, 2018).
Machado, M. C., Bellemare, M. G. & Bowling, M. A Laplacian framework for option discovery in reinforcement learning. In Proc. International Conference on Machine Learning (ICML) (eds. Precup, D. & Teh, Y. W.) Vol. 5, 3567–3582 (PMLR, 2017).
Pathak, D., Agrawal, P., Efros, A. A. & Darrell, T. Curiosity-driven exploration by self-supervised prediction. In Proc. 34th International Conference on Machine Learning (ICML) (eds. Precup, D. & Teh, Y. W.) 2778–2787 (PMLR, 2017).
Schillaci, G. et al. Intrinsic motivation and episodic memories for robot exploration of high-dimensional sensory spaces. Adaptive Behav. 29 549–566 (2020).
Colas, C., Fournier, P., Sigaud, O., Chetouani, M. & Oudeyer, P.-Y. CURIOUS: intrinsically motivated modular multi-goal reinforcement learning. In Proc. International Conference on Machine Learning (ICML) (eds. Chaudhuri, K. & Salakhutdinov, R.) 1331–1340 (PMLR, 2019).
Hafez, M. B., Weber, C., Kerzel, M. & Wermter, S. Improving robot dual-system motor learning with intrinsically motivated meta-control and latent-space experience imagination. Robot. Auton. Syst. 133, 103630 (2020).
Yamamoto, K., Onishi, T. & Tsuruoka, Y. Hierarchical reinforcement learning with abductive planning. In Proc. ICML/IJCAI/AAMAS 2018 Workshop on Planning and Learning (PAL-18) (2018).
Wu, B., Gupta, J. K. & Kochenderfer, M. J. Model primitive hierarchical lifelong reinforcement learning. In Proc. International Joint Conference on Autonomous Agents and Multiagent Systems (AAMAS) (eds. Agmon, N. et al.) Vol. 1, 34–42 (IFAAMAS, 2019).
Li, Z., Narayan, A. & Leong, T. Y. An efficient approach to model-based hierarchical reinforcement learning. In Proc. 31st AAAI Conference on Artificial Intelligence 3583–3589 (AAAI, 2017).
Hafner, D., Lillicrap, T. & Norouzi, M. Dream to control: learning behaviors by latent imagination. In Proc. International Conference on Learning Representations https://openreview.net/pdf?id=S1lOTC4tDS (ICLR, 2020).
Deisenroth, M. P., Rasmussen, C. E. & Fox, D. Learning to control a low-cost manipulator using data-efficient reinforcement learning. In Robotics: Science and Systems VII (RSS) (eds. Durrant-Whyte, H. et al.) 57–64 (Robotics: Science and Systems Foundation, 2011).
Ha, D. & Schmidhuber, J. Recurrent world models facilitate policy evolution. In Proc. 32nd International Conference on Neural Information Processing Systems (NeurIPS) (eds. Bengio, S. et al.) 2455–2467 (NIPS, 2018).
Battaglia, P. W. et al. Relational inductive biases, deep learning and graph networks. Preprint at https://arxiv.org/abs/1806.01261 (2018).
Andrychowicz, M. et al. Hindsight experience replay. In Proc. Neural Information Processing Systems (NIPS) (eds. Guyon I. et al.) 5048–5058 (NIPS, 2017); https://papers.nips.cc/paper/7090-hindsight-experience-replay.pdf
Schwartenbeck, P. et al. Computational mechanisms of curiosity and goal-directed exploration. eLife 8, e41703 (2019).
Haarnoja, T., Zhou, A., Abbeel, P. & Levine, S. Soft actor-critic: off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proc. International Conference on Machine Learning (ICML) (eds. Dy, J. & Krause, A.) 1861–1870 (PMLR, 2018).
Yu, A. J. & Dayan, P. Uncertainty, neuromodulation and attention. Neuron 46, 681–692 (2005).
Baldwin, D. A. & Kosie, J. E. How does the mind render streaming experience as events? Top. Cogn. Sci. 13, 79–105 (2021).
(参考文献可上下滑动查看)