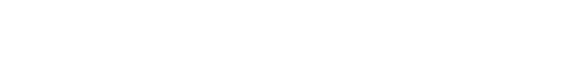原文链接:https://mp.weixin.qq.com/s/tMOm28SCjvCEXpjX_eJZyQ
作者马少平
第一篇 神经网络是如何实现的(三)
清华大学计算机系 马少平
第三节:神经网络是如何训练的
小明听艾博士介绍说,一个神经网络用不同的数据做训练,就可以识别不同的东西,感到很神奇,十分好奇地对艾博士说:艾博士,请您说说神经网络究竟是怎么训练的吧?
艾博士十分欣赏小明的好奇心,说道:好的,下面我们就开始介绍神经网络究竟是如何进行训练的。小明,你先说说,你是如何认识动物的?
小明回答说:小时候,每当看到一个小动物时,妈妈就会告诉我这是什么动物,见得多了,慢慢地就认识这些小动物了。难道神经网络也是这么认识动物的吗?
艾博士说:是的,神经网络也是通过一个个样本认识动物的。人很聪明,见到一次猫,下次可能就认识这是猫了,但是神经网络有点笨,需要给他大量的样本才可能训练好。比如我们要建一个可以识别猫和狗两种动物的神经网络,首先需要收集大量的猫和狗的照片,不同品种、不同大小、不同姿势的照片都要收集,并标注好哪些照片是猫,哪些照片是狗,就像妈妈告诉你哪个是猫哪个是狗一样。这是训练一个神经网络的第一步,数据越多越好。其实我们人类有时候也会这么做,所谓的“熟读唐诗三百首、不会作诗也会吟”,说的就是这个道理,所谓的见多识广。
准备好数据之后,下一步就要进行训练了。所谓训练,就是调整神经网络的权重,使得当输入一个猫的照片时,猫对应的输出接近于1,狗对应的输出接近于0,而当输入一个狗的照片时,狗对应的输出接近于1,猫对应的输出接近于0。
小明:如何做到这一点呢?
艾博士接着对小明说:我们先来举个例子。小明,你每天是不是要洗澡?洗澡时,你是怎么调节热水器的温度的?
小明不解地看着艾博士,心想我在问神经网络是怎么训练的,怎么说起洗澡了?不知道艾博士这葫芦里卖的什么药。但既然艾博士问到了,只好回答说:这个很容易啊,热水器上有两个旋钮阀门,一个调节热水,一个调节冷水,如果感觉水热了,就调大冷水,如果感觉水冷了,就调大热水。
艾博士又问道:感觉水热时也可以调小热水,感觉水冷是也可以调小冷水,对不对?
小明一想也确实这样,回答道:是的,有不同的调整方法,究竟调整哪个可能还需要看水量的大小。比如感觉水热了,但是水量也很大,这时就可以调节热水变小,如果水量不够大,则可以调节冷水变大。总之要根据水温和水量两个因素进行调节。
艾博士见小明终于说到点子上了,在肯定了他的说法之后又说:其实还有个调节大小的问题,如果感觉水温与自己的理想温度差别比较大,就一次把阀门多调节一些,如果差别不大就少调节一些,经过多次调整之后,就可以得到比较理想的水温和水量了。

图1.9 热水器调节示意图
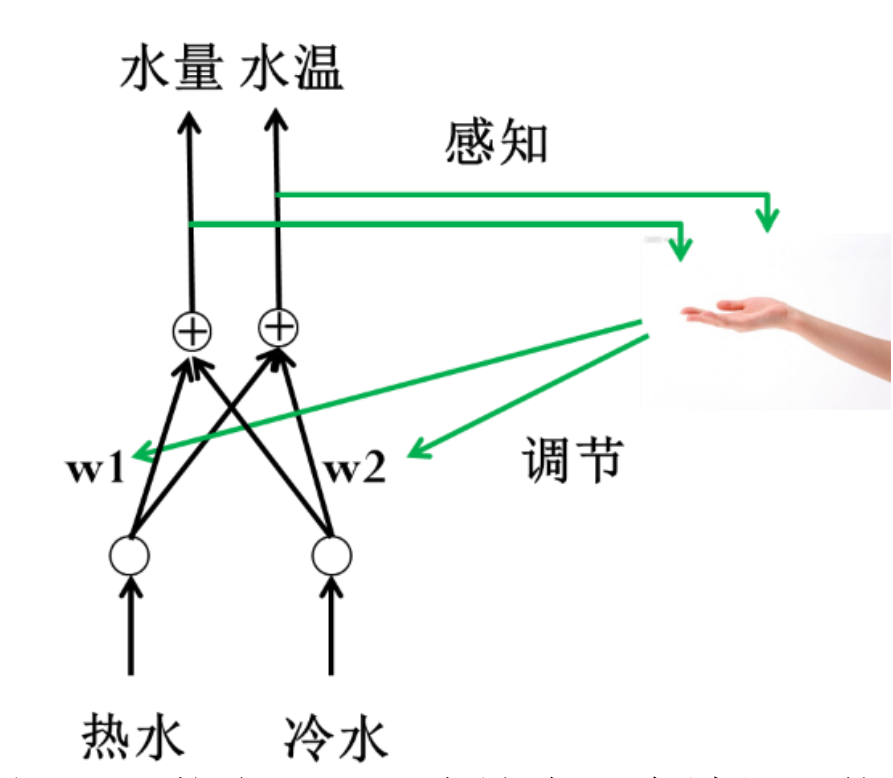
图1.10 热水器可以表达为一个神经网络
艾博士对小明说:我们可以把热水器抽象成图1.10,你看看这是不是就是一个神经网络?
小明用手拍着自己的小脑瓜说:我终于明白了,这确实就是一个神经网络。两个输入是热水和冷水,冷热水的两个阀门大小相当于权重,冷热水汇合的地方就相当于加权求和,最后从莲蓬头出来的水相当于两个输出,一个是水温,一个是水量。
那么调整冷热水阀门的大小是不是就相当于训练呢?小明歪着小脑瓜又问道。
艾博士回答说:正是这样的。调整水阀门的时候可以向大调也可以向小调,这是调整的方向,也可以一次调整的多一些,也可以调整的小一些,这是调整量的大小,还有就是调整哪个阀门,或者两个阀门都调整,但是大小和方向可能是不同的。
小明感慨到:没想到,我们每天洗澡时调整洗澡水这么简单的事情还有这么多的学问。那么这个思想如何用到训练神经网络上呢?
艾博士说:小明,在回答如何训练神经网络之前,我们先说说如何评价一个神经网络是否训练好了,这与训练神经网络是紧密相关的。在前面热水器的例子中,什么情况下你会认为热水器调节好了?
小明回答说:如果我觉得水温和水量跟我希望的差不多,就认为调节好了。
艾博士说:没错。但是对于计算机来说,什么叫差不多呢?需要有个衡量标准。比如我们用 水温 表示希望设定的水温,而用 水温 表示实际的水温,用 水量 表示希望的水量,用 水量 表示实际的水量,这样就可以用希望值与实际值的误差来衡量是否“差不多”,即当误差比较小时,则认为水温和水量调节的差不多了。但是由于误差有可能是正的(实际值小于希望值时),也可能是负的(实际值大于希望值时),不方便使用,所以我们常常用输出的“误差平方和”作为衡量标准。如下式所示:
阀门(水温水温)(水量水量)
其中E是阀门大小的函数,通过适当调节冷、热水阀门的大小,就可以使得E取得比较小的值,当E比较小时,就认为热水器调节好了。这里的“阀门”就相当于神经网络的权值w。
对于一个神经网络来说,我们假定有M个输出,对于一个输入样本d,用 表示网络的M个实际输出值,这些输出值对应的目标输出值为 ,对于该样本d神经网络输出的误差平方和可以表示为:
这是对于某一个样本d的输出误差平方和,如果是对于所有的样本呢?只要把所有样本的输出误差平方和累加到一起即可,我们用E(w)表示:
这里的N表示样本的总数。我们通常称E(w)为损失函数,当然还有其他形式的损失函数,误差平方和只是其中的一个。这里的w是一个由神经网络的所有权重组成的向量。神经网络的训练问题,就是求得合适的权值,使得损失函数最小。
小明看着公式困惑地问到:艾博士,一个神经网络有那么多的权值,这可怎么求解啊?
艾博士回答说:这确实是一个复杂的最优化问题。我们先从一个简单的例子说起,假定函数f(θ)如图1.11所示 ,该函数只有一个变量θ,我们想求它的最小值,怎么计算呢?
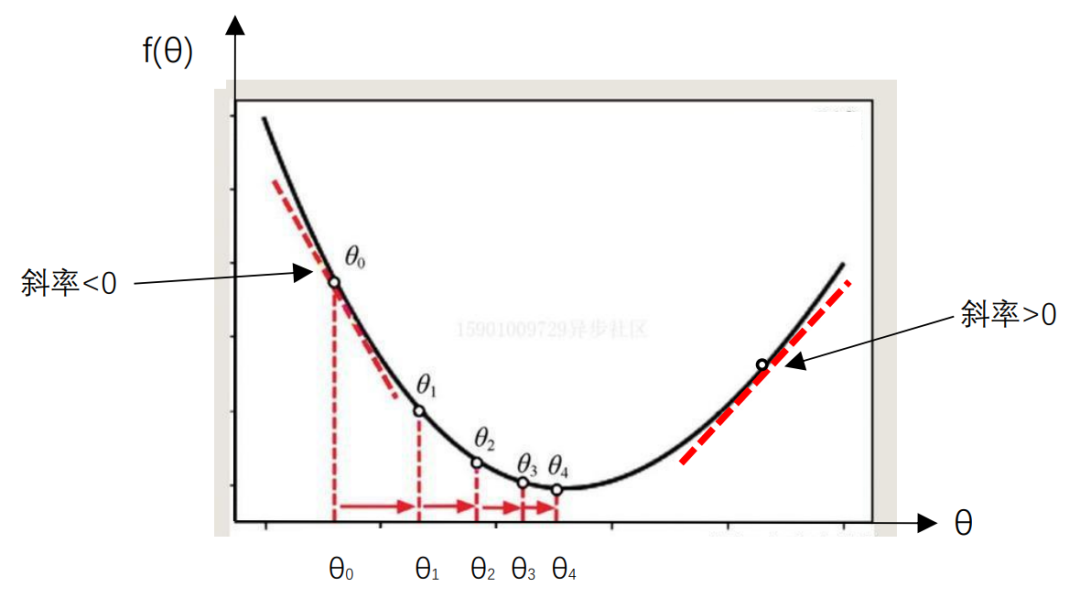
图1.11 最小值求解示意图
基本想法是,开始我们随机地取一个 值为 ,然后对 进行修改得到 ,再对 做修改得到 ,这么一步步地迭代下去,使得 一点点接近最小值。
假设当前值为 ,对 的修改量为 ,则:
如何计算 呢?有两点需要确定:一个是修改量的大小,一个是修改的方向,即加大还是减少。
小明你看图1.11,在图的两边距离最小值比较远的地方比较陡峭,而靠近最小值处则比较平缓,所以在没有其他信息的情况下,有理由认为,越是陡峭的地方距离最小值就越远,此处对 的修改量应该加大,而平缓的地方则说明距离最小值比较近了,修改量要比较小一些,以免越过最小值点。所以修改量的大小,也就是 的绝对值,应该与该处的陡峭程度有关,越是陡峭修改量越大,而越是平缓则修改量越小。
小明请你说说,如何度量曲线某处的陡峭程度呢?
小明很快地回答到:艾博士,我们学过函数的导数,在某一点的导数就是曲线在该点切线的斜率,斜率的大小直接反应了该处的陡峭程度。是不是可以用导数值作为曲线在某点陡峭程度的度量呢?
艾博士说:小明真是一个善于思考的好孩子!导数确实反应了曲线在某点的陡峭程度。接下来的问题就是如何确定θ的修改方向,也就是θ是加大还是减小。
艾博士指着图1.11问小明:在最小值两边的导数有什么特点呢?
小明想了想学过的高等数学知识,回答道:就像前面说过的,在某一点的导数就是曲线在该点切线的斜率,我们看图1.11的左半部分,曲线的切线是从左上到右下的,其斜率也就是导数值是小于0的负数,而在图1.11的右半部分,曲线的切线是从左下到右上的,其斜率也就是导数值是大于0的正数。
艾博士接着小明的话说:左边的导数值是负的,这时θ值应该加大,右边的导数值是正的,这时θ值应该减小,这样才能使得θ值向中间靠近,逐步接近f(θ)取值最小的地方。所以,θ的修改方向刚好与导数值的正负号相反。因此,我们可以这样修改θi值:
其中 表示函数f(θ)的导数。
小明听着艾博士的讲解,兴奋的说:这样求最小值的问题就解决了吧?
艾博士回答说:还有一个问题,如果导数值比较大可能会使得修改量过大,错过了最佳值,出现如图1.12所示的“震荡”,降低了求解效率。

图1.12 当步长过大时可能会产生震荡
小明摸了摸自己的头问道:那可怎么办呢?
艾博士说:一种简单的处理办法是对修改量乘以一个叫做步长的常量η,这是一个小于1的正数,让修改量人为地变小。也就是:
步长η需要选取一个合适的值,往往根据经验和实验决定。也有一些自动选择步长,甚至变步长的方法,我们今天先不讲了,如果有兴趣可以阅读相关材料。
小明问艾博士:神经网络也是这样训练的吗?
艾博士说:基本原理是一样的。小明你还记得训练神经网络我们要优化的目标吗?
小明回答说:记得啊,就是求误差平方和的最小值,也就是前面讲过的损失函数E(w)的最小值。
艾博士说:我们可以用同样的方法求解E(w)的最小值,所不同的是E(w)是一个多变量函数,所有的权重都是变量,都要求解,每个权重的修改方式与前面讲的θ的修改方式是一样的,只是导数要用偏导数代替。如果用wi表示某个权重的话,则采用下式对权重 进行更新:
其中 、 分别表示 修改前、修改后的值, 表示E(w)对 的偏导数。所有对 的偏导数组成的向量称为梯度,记作 :
所以对所有w的修改,可以用梯度表示为:
这里的 、 、 、 均为向量, 是常量。两个向量相加为对应元素相加,一个常量乘以一个向量,则是该常量与向量的每个元素相乘,结果还是向量。
小明看着梯度符号问艾博士:艾博士,这里的梯度物理含义是什么呢?
艾博士回答说:如同只有一个变量时的导数表示函数曲线在某个点处的陡峭程度一样,梯度反应的是多维空间中一个曲面在某点的陡峭程度。就如同我们下山时,每次都选择我们当前站的位置最陡峭的方向一样。所以这种求解函数最小值的方法又称作梯度下降算法。
小明又问道:艾博士,这样看来,要训练神经网络,主要问题就是如何计算梯度了?
艾博士回答说:确实是这样的。对于神经网络来说,由于包含很多在不同层的神经元,计算梯度还是有些复杂的。在计算时,也分三种情况,一种是这里所说的标准梯度下降方法。在计算梯度时要用到所有的训练样本,一般来说训练样本量是很大的,每更新一次权重都要计算所有样本的输出,计算量会比较大。另一种极端的方法是,对每个样本都计算一次梯度,然后更新一次权重,这种方法称为随机梯度下降。由于每个样本都调整一次w的值,所以计算速度会比较快,一般情况下可以比较快地得到一个还不错的结果。在使用这个方法时,要求训练样本要随机排列,比如训练一个识别猫和狗的神经网络,不能前面都用猫训练,后面都用狗训练,而是猫和狗随机交错地使用,这样才可能得到一个比较好的结果。这也是随机梯度下降算法这一名称的由来。
小明:这倒是一个比较好的方法,但是这样一次只用一个样本是否会存在问题呢?
艾博士:确实存在问题。随机梯度下降方法在训练的开始阶段可能下降的比较快,但在后期,尤其是接近最小值时,可能效果并不好,毕竟梯度是由一个样本计算得到的,并不能代表所有样本的梯度方向。另外就是可能有个别不好的样本,甚至标注错了的样本,会对结果产生比较大的影响。
说到这里艾博士又问小明:小明,我们说了两种情况,一种是一次用上全部样本,一种是一次只用一个样本,你想想是否可以有折中的办法呢?
小明歪着小脑瓜回答说:折中的办法么……,既不是用全部,也不是用一个,那就是一次用一部分了?
艾博士高兴地看着小明说:是的,介于上述两种方法之间的一种方法是每次用一小部分样本计算梯度,修改权重w的值。这种方法称作小批量梯度下降算法,是目前用的最多的方法。
小明说:知道了这三种方法,但是还是不知道梯度如何计算啊?
艾博士说:小明你别着急,我们马上就讲梯度的计算方法。其实以上三种方法只是计算时用的样本量有所不同,梯度的计算方法是差不多的,为了简单起见,我们以随机梯度下降算法为例说明,很容易推广到梯度下降算法或者小批量梯度下降算法。
下面我们以随机梯度下降算法为例给出具体的算法描述,想了解如何得到这个算法的话,请参考有关材料。
利用随机梯度下降算法训练神经网络,就是求下式的最小值:
其中d为给定的样本,M是输出层神经元的个数, 是样本d希望得到的输出值, 是样本d的实际的输出值。
为了叙述方便,对于神经网络中的任意一个神经元j,我们约定如下符号:神经元j的第i个输入为 ,相对应的权重为 。这里的神经元j可能是输出层的,也可能是隐含层的。 不一定是神经网络的输入,也可能是神经元j所在层的前一层的第i个神经元的输出,直接连接到了神经元j。我们得到随机梯度下降算法如下:
算法 随机梯度下降算法:
1、神经网络的所有权值赋值一个比较小的随机值如[-0.05, 0.05]
2、在满足结束条件前:
3、 对于每个训练样本
4、 把样本输入神经网络,从输入层到输出层,计算每个神经元的输出
5、 对于输出层神经元k,计算误差项:
6、对于隐含层神经元h,计算误差项:
后续
7、更新每个权值:
其中算法第二行的结束条件,可以设定为所有样本中最大的 小于某个给定值时,或者所有样本中最大的 小于给定值时,算法结束。
小明指着算法第6行问艾博士:这里公式中的“ 后续 ”是什么意思呢?
艾博士解释说:h是隐含层的神经元,它的输出会连接到它的下一层神经元中,“后续(h)”指的是所有的以h的输出作为输入的神经元,对于全连接神经网络来说,就是h所在层的下一层的所有神经元。
第6行公式中:
后续
就是用h的每个后续神经元的误差项 乘以h到神经元k的输入权重,再求和得到。
小明弄清楚了这些符号的意义后又问艾博士:艾博士,这个算法看起来像是从输出层开始,先计算输出层每个神经元的 值,有了 值,就可以对输出层神经元的权重进行更新。然后再利用输出层神经元的 值,计算其前一层神经元的 ,这样就可以更新前一层的神经元的权重,这样一层层往前推,每次利用后一层的 值计算前一层的 值,就可以实现对所有神经元的权重更新了,真是巧妙。
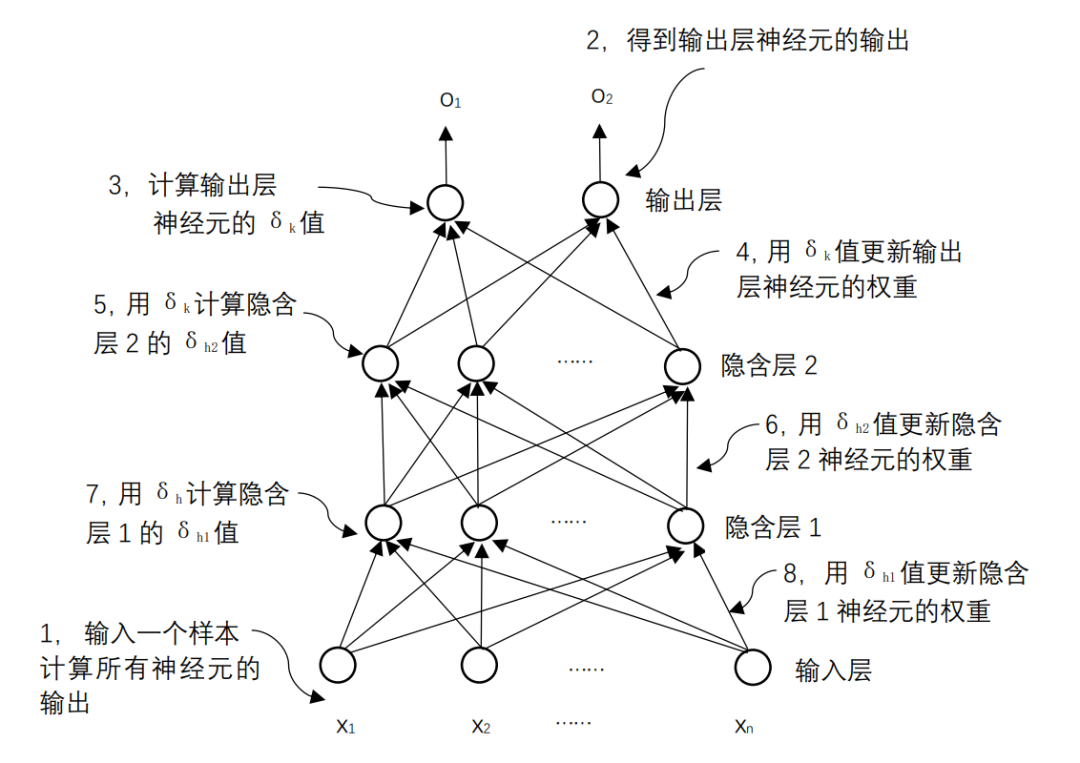
图1.14 BP算法计算过程示意图
艾博士说:小明分析的非常正确。当给定一个训练样本后,先是利用当前的权重从输入向输出方向计算每个神经元的输出值,然后再从输出层开始反向计算每个神经元的δ值,从而对每个神经元的权重进行更新。如图1.14所示。正是由于采用这样一种反向一层层向前推进的计算过程,所以它有个名称叫“反向传播算法”,简称BP(Backpropagation Algorithm)算法。该算法也是神经网络训练的基本算法,不只是可以训练全连接神经网络,到目前为止的任何神经网络都是采用这个算法,只是根据神经网络的结构不同,具体计算上有所差别。
艾博士又强调说:前面介绍的随机梯度算法中的具体计算方法,是在损失函数采用误差平方和,并且激活函数采用sigmoid函数这种特殊情况下推导出来的,如果用其他的损失函数,或者用其他的激活函数,其具体的计算方法都会有所改变,这一点一定要注意。
听到这里,小明问道:我已经知道有多种不同的激活函数,但是还有其他的损失函数吗?
艾博士回答说:还有一种常用的损失函数叫交叉熵损失函数,其表达式如下:
这是对于一个样本d的损失函数,如果是对于所有的样本,则为:
其中 表示样本d在输出层第k个神经元的希望输出, 表示样本d在输出层第k个神经元的实际输出, 表示对输出 求对数。
小明看着公式不明白地问到:交叉熵损失函数有什么具体的物理含义吗?
艾博士反问小明:你还记得我们前面以猫、狗识别举例时,神经网络的希望输出是什么样子吗?
小明想了想回答道:一个输出代表猫,一个输出代表狗。当输入为猫时,代表猫的输出希望为1,另一个希望为0,而当输入为狗时,则是代表狗的输出希望为1,另一个希望为0。
艾博士说:对。这里的希望输出1或者0,可以认为就是概率值。
小明问到:我们如何在神经网络输出层获得一个概率呢?
艾博士:如果在输出层获得概率值,需要满足概率的两个主要属性,一个是取值在0和1之间,另一个是所有输出累加和为1。为此需要用到一个名为softmax的激活函数。该激活函数与我们介绍过的只作用于一个神经元的激活函数不同,softmax作用在输出层的所有神经元上。
设 、、 分别为输出层每个神经元未加激活函数的输出,则经过softmax激活函数之后,第i个神经元的输出 为:
很容易验证这样的输出值可以满足概率的两个属性。这样我们就可以将神经网络的输出当作概率使用了,后面我们会看到这种用法非常普遍。
艾博士继续讲解说:我们再回到你问的交叉熵损失函数的物理意义这个问题上来。从概率的角度来说,我们就是希望与输入对应的输出概率比较大,而其他输出概率比较小。对于一个分类问题,当输入样本给定时,M个希望输出中只有一个为1,其他均为0,所以这时的交叉熵中求和部分实际上只有一项不为0,其他项均为0,所以:
我们求 最小,去掉负号实际就是求 最大,也就是求样本d对应输出的概率值 最大。由于输出层用的是softmax激活函数,输出层所有神经元输出之和为1,样本d对应的输出变大了,其他输出也就自然变小了。
小明:原来是这个含义啊,我明白了。那么误差平方和损失函数和交叉熵损失函数各有什么用处呢?
艾博士:小明你这个问题问的非常好。从上面的分析看,交叉熵损失函数更适合于分类问题,直接优化输出的概率值。而误差平方和损失函数比较适合于预测问题。
小明不明白什么是预测问题,马上问道:艾博士,什么是预测问题呢?
艾博士举例说:如果输出是预测某个具有具体大小的数值,就是预测问题。比如说,我们根据今天的天气情况,预测明天的最高气温,就属于预测问题,因为我们预测的是气温的具体数值。
经过艾博士的认真讲解,小明终于明白了什么是神经网络,以及神经网络的训练方法,跟艾博士道别后,带着满满的收获回家了。