原文链接:https://mp.weixin.qq.com/s/0H0jp3hmZiu_n3zAYQJHIA
梁金、李旭 集智俱乐部
导语
在椋鸟、细菌群落、蚁群、绵羊等不同尺度生命系统中,都可以观察到集体行为。由大量个体组成的群体中如何涌现出集体行为?这些集体行为背后有什么普遍规律?集体行为之间的转变是否为相变,要如何描述这些相变及确定其属性?近日,北京师范大学系统科学学院陈晓松、李旭等人,利用本征微观态方法,发现集体运动的Vicsek模型中存在着两种相变。通过本征微观态与序参量有限尺度标度分析,识别了相变的属性,一种是密度的不连续相变,另一种是集体运动的连续相变。
研究领域:生命复杂性,非平衡系统,集体运动,相变
梁金、李旭 | 作者
陈晓松 | 审校
邓一雪 | 编辑

论文题目:Discontinuous and continuous transitions of collective behaviors in living systems 论文地址:http://cpb.iphy.ac.cn/EN/10.1088/1674-1056/ac3c3f
1. 集体运动与Vicsek模型
生命系统充满了令人惊叹的多样性和复杂性。例如,在椋鸟、细菌群落、蚁群、蝗虫、绵羊等由大量个体组成的群体中,尽管这些系统的尺度和认知能力存在巨大差异,却都可以观察到集体行为。
与生物学家一般喜欢详细研究具体案例不同,物理学家则更热衷于探寻纷繁现象背后的普遍特征,通过建立模型寻找集体行为背后的基本原理。从系统个体的微观性质出发,利用概率论和统计学得到系统的宏观性质,是统计物理学的使命。在相变和临界现象的研究中,关键物理量是由著名物理学家朗道提出的序参量。例如,气液相变的序参量是密度差,铁磁相变的序参量是磁化强度。许多复杂系统相变与临界现象的序参量非常复杂,难以事先确定,给研究其相变与临界现象带来巨大的困难和挑战。
Vicsek模型[1]是研究生命系统集体运动的一个简约模型,由自我推进的点状粒子组成。在强噪声或低密度时,粒子总体上随机运动,整个系统就像是无序的气体。而在高密度或低噪声情况下,粒子的速度倾向于与相邻粒子保持一致,整体朝向同一个方向运动,从而涌现出集体运动,经历从无序到有序的相变。
在提出Vicsek模型的原文中,上述群体运动的相变被认为是连续的[1]。但后续进一步研究对这一观点提出了质疑,这些研究者认为,Viscek等人观测到的连续相变实际上是由于有限尺寸效应(finite-size effect)导致的,集体运动的相变实际上是不连续的[2]。由于这些研究不能采用集体运动相变精确的序参量,也没有进行有限尺度标度性的系统分析,它们关于相变性质的结论无法成为定论。
2. 本征微观态方法研究生命系统
对于大量需要研究的复杂系统,其能量函数、系统状态分布函数和序参量都是未知。但通过实验测量或计算模拟,我们可以获得系统每个个体状态的时间序列。通过最近提出的本征微观态方法[3],复杂系统的相变与临界现象可通过本征微观态的凝聚来确定,这类似于玻色气体的玻色-爱因斯坦凝聚,即宏观数量玻色子在极低温下处于基态能级。此方法已被成功应用于伊辛模型的铁磁相变、地球温度系统、股票市场[3]。
现在,本征微观态方法被应用于生命系统。对于N个个体组成的生命系统,我们已知每个个体的速度和位置时间序列,系统微观态由个体的速度和邻近密度描述。采用本征微观态方法,可以得到生命系统的本征微观态 uI,及对应的序参量 σI。随着生命系统遭遇外部或内部扰动产生的噪声变弱,序参量 σI可能会从 0 增加到一个有限值,本征微观态出现凝聚,生命系统发生相变、涌现出本征微观态 uI刻画的相。
在临界点附近,σI遵循有限尺寸标度形式(finite-size scaling form):

这里 L 是系统的尺寸,是约化噪声,β 是序参量 σI的临界指数,ν 是关联长度的临界指数。β>0 时,系统发生连续相变;β=0 时,序参量出现跳变,系统发生不连续相变。
3. 集体运动的连续和不连续相变
最近,本征微观态方法被用于研究Vicsek模型的相变与临界现象。当系统处在强噪声环境的时候,粒子的位置和速度方向都是随机的,它们的本征微观态也没有哪个占据主导,系统处于无序状态。
随着噪声降低,第一大本征微观态的序参量 σ1变为有限,系统涌现出一个新的相,即本征微观态 u1 ,对应的临界指数 β=0。如图1所示,随着噪声减弱,粒子之间的有效相互作用增强,彼此之间距离变小,平均邻近密度增大;噪声减小到某个值的时候,与气-液相变相似,系统会发生一个密度的不连续相变。
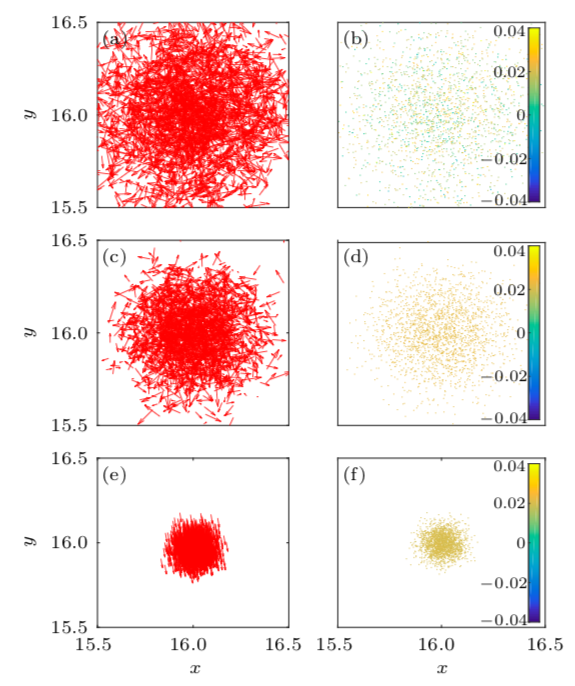
图1. 从上到下为噪声 η=6, 3.95, 0.25 时,第一大本征微观态 u1的速度空间分布(a, c, e)和邻近密度涨落(b, d, f)。当噪声 η1c=3. 95 时,平均邻近密度增大,粒子发生凝聚,系统经历密度的非连续相变。
在更小的噪声环境下,如图2所示,由于邻近密度进一步增大,粒子之间的有效相互作用继续增强,从而导致粒子速度方向趋向一致,系统发生集体运动的相变。通过有限尺度标度性分析,得到临界指数 β>0,因此该集体运动相变是连续的。此相变发生时,系统同时涌现两个序参量相同、速度方向相互垂直的本征微观态 u2 和 u3 。
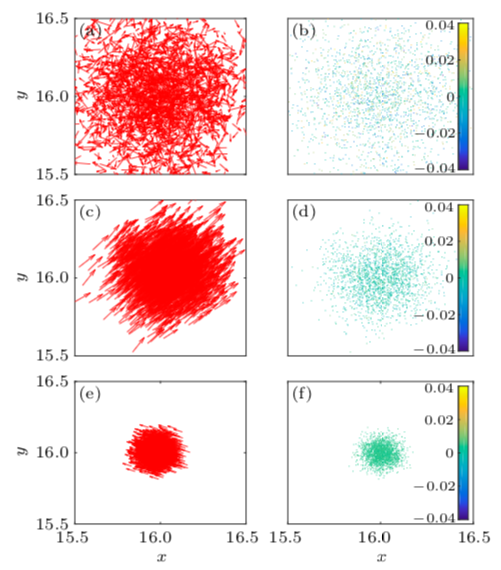
图2. 噪声 η=6, 3.69, 0.25 时,第二大本征微观态 u2的速度空间分布(a, c, e)和邻近密度涨落(b, d, f)。当噪声 η2c=3.69 时,粒子速度方向变得一致,系统经历连续相变。
上述研究表明,由Vicsek模型描述的非平衡生命系统能够出现两种相变。随着噪声减弱,首先发生密度主导的气-液不连续相变,导致粒子间距减小、相互作用增强,然后粒子状态(速度)趋同,发生集体运动的连续相变。利用有限尺度标度性,得到不同Vicsek模型连续相变的临界指数相同,表明它们属于同一个普适类。这里发现的相变机制与特性对生命系统可能具有普遍性。
本征微观态方法在生命系统的成功应用,表明其对于非平衡态的适用性。未来还可将其应用于更广泛的复杂系统,比如气候系统、生态系统和流体系统等。
以上结果作为 Rapid Communication 发表在 Chin. Phys. B 30, 128703 (2021).
参考文献
[1] Vicsek T, Czirok A, Ben-Jacob E, Cohenl I, and Shochet O 1995 Phys. Rev. Lett. 75, 1226.
[2] Gregoire G and Chate H 2004 Phys. Rev. Lett. 92, 025702.
[3] Sun Y, Hu G, Zhang Y, Lu B, Lu Z, Fan J, Li X, Deng Q, and Chen X 2021 Commun. Theor. Phys. 73, 065603.