原文链接:https://mp.weixin.qq.com/s/hpyH8nUYiXgG8AQ5fYhr2A
原创 乔建永
人机与认知实验室
编者按:当前人工智能不可解释性依然成为制约其发展的关键与瓶颈,本文从逻辑推理的角度深入探讨了AI“不可读”的根源,即人们通过计算机和人工智能把一系列逻辑推理压缩在一次逻辑推理里,造成了自然人的“不可读”。同时,在剖析数学领域三次危机的过程中,探讨了构建庞大的逻辑推理网络动力系统对AI的必要性和可行性,进而通过疫情预测事例,提出“从尺规作图到机器证明”的大逻辑解决思想。

随着人工智能科技的迅猛发展,一个幽灵般的问题开始在人们的头脑中徘徊:机器人能被训练成数学家吗?这一问题关系到哲学的基本问题。笔者以为,机器证明同尺规作图一样都是数学家借助辅助工具实施逻辑推理的过程,机器人、计算机和直尺、圆规等无疑是逻辑推理的辅助工具,而数学家是逻辑推理的主体。

所谓逻辑推理,是自然人由一个或几个已知的判断推导出一个新的判断的思维形式。人类从远古走来,正是靠这种方式,一步一步迭代,构建起庞大的推理型知识体系,支撑起当代人类文明。本文无意深入考察逻辑推理的科学和哲学内涵,而是探讨现有知识点之间的逻辑关系,建立推理型知识的网络动力系统模型,通过分析其动力机制,揭示快速计算和人工智能等新技术作为逻辑推理辅助工具的本质属性。

一、推理型知识网络及其演化动力
逻辑推理是产生新知识的一种重要方式。知识是人类通过各种途径获得的,经过提升、总结和凝练的系统认识。获取知识的复杂过程主要包括感觉、交流和推理。柏拉图认为,一条陈述能称得上是知识必须满足三个条件,它一定是被验证过的,正确的,而且是被人们相信的,这也是科学与非科学的区分标准。本文把知识进一步限定为人类通过逻辑推理获取的知识,没有通过逻辑推理而存在的“知识”暂且不叫知识。显然,推理型知识体系是无数个关联的知识点的集合,其中数学就是一个逻辑推理的知识体系,代数、几何、分析等各个分支也相对独立地构成子体系。如果我们把这些大大小小的知识点看作“点”,然后按照逻辑推理的新老关系用有向“边”连接起来,就构成了一个推理型知识网络。这个网络系统随着人类日复一日的逻辑推理在不断的演化——扩张、简约、纠错,没有最好,只有更好。
推动这个网络系统演化的唯一动力是人类的逻辑推理。某个自然人由一个或几个已知的知识点推出一个新的知识点,这个网络就增加了一个节点;当有人发现一些既有的节点之间的因果关系可以简化时,还可以用推理把这个网络进一步简约化;推理也可能发现老节点之间因果关系的错误,予以删除,实现这个网络的纠错。
我们特别强调,这个网络系统中的每一个节点都是某一个自然人通过逻辑推理得到的,因此,这一网络的局部特征就同自然人的生命长度和生理功能密切相关。任何一个节点以及同此点直接连接的所有节点代表的逻辑关系能够被一个自然人独立推导、阅读或审核,本文将这一性质称为自然人的局部可读性。
为了进一步解释这一网络的局部可读性,我们解剖一个具体数学问题:求前 100个自然数之和。解决这个问题最初等的推理是按自然数顺序依次做 99 次加法运算,最终计算出结果;考虑到上面的推理用时较长,高斯观察到 1+ 100, 2 + 99, ……, 50 + 51 的值全是 101,因此上式之和为101 与 50 的积,故等于 5050。毫无疑问,高斯的办法大大减少了推理的时间和推理语言占用的空间。仅仅针对这个小问题可见,自然人在生命时长内和在生理功能允许的范围内能否推导出希望的新结果,因人而异。但如果把问题改为求前10 亿个自然数之和的问题,你就会发现不同推理方法的更多的价值。首先注意,如果试图用初等推理方法解决这个问题(也就是按自然数顺序依次做加法的运算),将用时太长,一个自然人在其生命时间里无法完成;但用高斯的上述方法却很美妙,把推理过程写下来很短,具有“可读性”。为了避免第一种方法“不可读” 的问题还有两种替代方法,一是把这一过长的计算截成若干段,让若干自然人接续按第一种方法计算,最终得到结果,这种方法相当于扩充了知识网络节点,虽然可能会用很长时间(或许需要数代人的接续),但每一步推理都具有可读性;二是汇聚一批人(几百、几千或几万人)同时分段、分层计算,能够加快计算速度,这同使用计算机是一个原理,这种方法虽然“可读性”比较差,但计算速度提高了。概括来讲,要解决自然人在生命长度内、在生理功能允许范围内不能完成的推理问题,有三种方法:用人的智力寻找新方法、把知识网络中的一个节点扩张为一系列节点、借助人的生理功能以外的推理工具。
推理型知识网络演化的动力来源于自然人,这是本文的基本观点,也是迄今为止这一网络演化遵从的基本规律。自然人的局部可读性有效保证了这一网络系统的严密性和可靠性。从历史的宏观尺度来审视,这一网络系统演化过程的随机性和复杂性同样巨大。注意到人的复杂性、多元化、个性化,即每个人的兴趣、需求、特长都不一样,由各个自然人推理过程决定的节点之间的关系一定是千差万别的。这一网络系统的演化必定会受生长机制和推理者个人偏好的影响。每个网络都是从几个称之为公理或假说的小节点开始,通过添加新的节点而增长。虽然这一网络系统的演化历史在某些时刻会因为某些天才的“离经叛道”而改写,但多数时候这些新节点在决定连向哪里时,推理者往往会倾向选择那些拥有更多连接的节点,这是一个宏观历史规律。
二、围绕推理长度与可读性的争论
推理与概念、判断一样,同语言密切联系在一起,推理的语言形式为表示因果关系的复句或具有因果关系的句群;推理用语言表达出来,一个自然人必须能够在其生命长度时间里审核其正确性,不能太长,这就是前面定义的可读性;这里要求的是一个自然人完整审核推理过程,而不是一群自然人在同一个逻辑层级上分工阅读,然后彼此互相提供证言;逻辑推理是一个迭代的过程,如同建筑工程一样,从泥土,砖头,墙壁,到楼房。承认一个前提推演新的结论,不能把一系列逻辑推理压缩在一次逻辑推理里,这样会造成自然人的“不可读”,两个独立的人能够分工对一次逻辑推理的正确性负责吗?答案显然是否定的,这关系到科学大厦的严密性和可靠性。
本文前面提到的求前 10亿个自然数之和的问题,如果用计算机解决问题,其实就是把若干自然人接续计算的若干次“可读型”逻辑推理压缩到计算机里。然而,视乎人们对此并不反感,因为人们对这种按部就班的加法运算太熟悉啦,以至于有点儿麻木。对那些人们确实陌生的问题,大家的态度会不会有变化呢?请看两个著名的例子。
第一个例子是四色猜想。1852年 10 月,英国有位刚大学毕业的青年人在给地图着色的过程中发现似乎只需要4 种颜色。1878 年 6月 13 日,英国数学家凯莱在伦敦数学会上正式提出四色猜想,同时发表于会议的论文集。从此,吸引了全世界的数学家致力于四色猜想的证明,但一直没能解决。
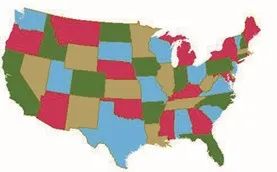
1976 年,阿贝尔和哈肯宣布用计算机证明了“四色猜想”。美国伊利诺伊地方邮局立刻用邮戳“Four colors suffice”表示了祝贺,但数学界并不满意。原因是,数学家不知道怎样检查他们证明的正确性(阿贝尔和哈肯用自己的程序工作了四年,花了 1200 个计算机小时,检查了 3000 多个数学结论);还有,这里“数学证明”的概念远不是数学家习惯的模样儿,发生了突变。
第二个例子是球堆积猜想。1590年的某一天,英国罗利爵士在考虑自己船队出海时船上炮弹码放方式,求助于英国数学家哈里耳特;哈里耳特将其规范为怎样码放球体,使其占用空间最小的问题,并写信告诉了德国科学家开普勒;1611 年开普勒提出球堆积猜想:当大小相当的球体按照“面心晶体”的形式,并且将第一层摆成六角形时,它们占用的空间最小,对空间的利用率可以超过74%。1900年,希尔伯特将这一猜想列入著名的“二十三个未解数学难题”。

1953 年,匈牙利数学家托斯得到结论:球堆积猜想的证明可以减少为有限多种情况(数目极为庞大)。从1992 年开始,美国密歇根大学的托马斯 •海尔斯按照托斯的思路用计算机研究球堆积猜想;经过 6 年运算,1998年海尔斯宣布完成证明。海尔斯的证明包括 250 页文稿,10万行左右的计算机程序,3G的计算机程序和运算结果。著名数学杂志 Ann of Math 起初表示同意发表海尔斯的证明,于是该杂志聘请托斯的儿子担任评审委员会的负责人,开始对海尔斯的证明进行彻底而审慎的检验。但是,审核了6 年后,评审委员会决定放弃全面验证该文的计划。无奈之下, Ann of Math提出发表时加一条免责条款:本证明大部分,但非全部,被验证过。因遭到许多数学家的批评而未实施。最后Ann of Math 决定:将论文一切两半,刊登已经使用传统方式验证过的证明,舍弃计算机运算的数据。
有人把这种逻辑推导与计算机辅助合成的“三明治”式的推导称为新潮数学。普林斯顿大学康威教授说:我不喜欢它们(计算机证明),因为不知道究竟发生了什么。也有乐观的数学家说:计算机可以打败世界象棋冠军,为什么不能战胜数学家?这样的争论或许还会延续很长时间。
三、围绕推理主体和推理工具的争论
如前所述,我们强调推理的主体是一个自然人,或能够相互完整阅读对方推理语言的若干个自然人;推理方案可以分解为若干子系统或分支,只能阅读和理解某一部分推理过程的人不能作为推理主体;推理主体可以借助一定的辅助工具,比如圆规、直尺、算盘,以及计算机、机器人,但它们不是推理主体;大量参与验算的人同机器验算本质上是一会儿事,这样的人不是推理主体。四色猜想的计算机证明用机器检查了海量的子情况,这样的工作其实可以按计划分配给几千人或几万人分头去做,难道可以写一篇作者数量为几万人的数学论文?!然而,近年来计算机的发展带来人工智能的新时代,数学界的一些例子时常带来新的争论。
数学家泽尔伯格是美国罗格斯大学教授。有传言,给他写电子邮件要加上 “Math Is Fun”,否则他的系统就可能会把邮件当做垃圾邮件过滤掉;他不喜欢开车,喜欢坐火车,因为坐火车可以同时研究数学。当今数学界有个作者艾卡德,他已经独立或同泽尔伯格合作发表了几十篇数学研究论文。泽尔伯格说自己是艾卡德(Shalosh B. Ekhad)的导师,但其实艾卡德是泽尔伯格操作的一台计算机。试问能独立发表数学论文的计算机是逻辑推理的主体吗?除非这篇论文里没有推理的问题。
仔细分析,计算机是否可以成为逻辑推理的主体,应该是一个实实在在的哲学问题,推理主体和推理模式一定是密切相关的。菜尔伯格与艾卡德合作过程中究竟谁主导的推理?这个问题可以用笛卡尔的“我思故我在”的哲学观点来分析。大家知道,笛卡尔被广泛认为是西方现代哲学的奠基人,他首创了一套完整的哲学体系。“我思故我在”是笛卡尔全部认识论哲学的起点,也是他“普遍怀疑”的终点。笛卡尔认为思考是唯一确定的存在。
关于推理模式的变革,不能不提维克托的著作《大数据时代》。维克托拥有在哈佛大学、牛津大学等多个互联网研究重镇任教的经历。有书评说:维克托最具洞见之处在于,他明确指出大数据时代最大的转变是放弃对因果关系的渴求,取而代之关注相关关系。也就是说只要知道“是什么”,而不需要知道 “为什么”。这就颠覆了千百年来人类的思维惯性,对人类的认知和与世界交流的方式提出了全新的挑战。
笔者以为维克托的上述迷失在于用局部代替了整体,忽视了更大范围的因果关系。事实上,快速计算加大了逻辑推理的“容量”,以演绎推理的三段式论证为例,大前提和小前提的语言表述借助计算机的功力可能实现几百G 的容量,但从宏观上看,三段式论证的结构并没有改变。

这或许是科学思维的一次维度拓展,从原来的二维(实证思维、逻辑思维)拓展为三维(实证思维、逻辑思维和大逻辑思维)。当前我们要解决的问题是:大逻辑思维的哲学意义,大逻辑体系的基本科学分类,以及大逻辑体系的判别标准。
2010 年,国际著名学术杂志 Nature 上刊登了华盛顿大学贝克尔教授一篇和游戏有关的科研论文,作者超过5700 人;2015 年物理学杂志 Phys Rev Lett 上一篇研究论文作者数量达到5154 ;2016 年 Phys Rev Lett 上还有一篇论文作者数量 1011,其中诞生了三位诺奖;最近,Nature 上有一篇论文,作者数量更是超过 6 万人。我不知道这些论文的推理细节,但我相信其中推理的主体应该只是少数几个人,大量的作者其实做的是类似于计算机的验证性辅助工作,或者其中并无推理过程。
四、推理型知识网络演化的奇点
前面我们系统阐述了人类靠逻辑推理,一步一步迭代,构建起庞大的逻辑推理网络动力系统。毫无疑问,每一次逻辑推理都是严密的,但这并不能保证整个网络光滑演化,这里光滑演化的含义是系统在演化过程中始终保持自洽,新结果同老结果没有矛盾。事实上,在数学的发展史上,既出现过推理节点突破人类认识的时刻,也出现过推理范围受限的时刻,这就是网络系统演化过程中出现的三个著名奇点:三次数学危机。
第一次数学危机称为毕达哥拉斯悖论,发生在公元前 5 世纪。当时在意大利半岛上有个毕达哥拉斯学派,他们信奉“万物皆数”的信条,号称任何线段长度都可表示为两个自然数之比。他们证明过有理数具有稠密性与和谐性,以及毕达哥拉斯定理(勾股定理)。毕达哥拉斯悖论是希帕索斯发现的,他发现了直角边长为1 的等腰直角三角形斜边长度不是自然数之比。

希帕索斯因此遭到毕达哥拉斯学派的追杀,后被扔进大海,成为第一次数学危机的殉葬品。大约公元前370 年,古希腊数学家尤得塞斯建立了新的比例理论,无理数被认识,才彻底化解了毕达哥拉斯悖论。第一次数学危机的启示:直觉不可靠,推理证明才是可靠的。从此,古希腊人从重视“计算技术”转向重视演绎推理,实现了数学思想的一次巨大革命。
第二次数学危机称为贝克莱悖论,发生在 18 世纪。17 世纪末,科学技术的发展催生了微积分,牛顿和莱布尼茨分别独立地建立了微积分方法。牛顿和莱布尼茨在求导数过程中引进了量dx。1734 年爱尔兰主教贝克莱提出:在牛顿和莱布尼茨求导数过程中,dx 既是 0又不是 0,这就是贝克莱悖论。
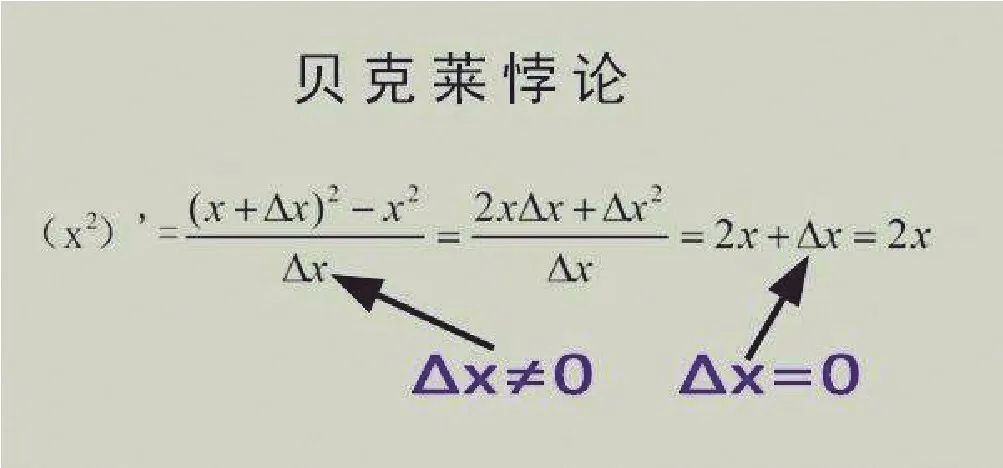
1820 年,法国数学家柯西提出极限论思想,把无穷小量规范为极限为零的变量。进一步,魏尔斯托拉斯给出极限的ε − δ 语言。贝克莱悖论才得到彻底解决,第二次数学危机化解。数学分析诞生。
第三次数学危机称为罗素悖论,发生在 20 世纪初。当时康托尔建立了集合论这一现代数学的基础,希尔伯特提出 23个数学问题,数学界喜气洋洋,一片乐观。1900 年庞加莱称:数学的严格性,看来直到今天才可以说是实现了。正在这时罗素定义了集合R :所有不以自己为元素的集合所组成的集合。大家知道,集合论有一个公认的基本原则:一个元素要么属于该集合,要么不属于该集合,二者必居其一。这一原则却受到罗素悖论的正面挑战:R 本身既是 R 的元素,又不是 R 的元素。

罗素把这一发现写信告诉了德国数学家弗雷格。弗雷格说:一个科学家所遇到的最不合心意的事,莫过于在他的工作即将结束时,其基础却崩塌了,罗素先生的一封信正好把我置于这个境地。罗素悖论引发了第三次数学危机。
为了解决罗素悖论,演化出逻辑主义、直觉主义、形式主义等数学学派,产生了集合论的公理化。主要思想都是对集合加以限制,排除悖论,保留所有有价值的东西。庞加莱说:我们建造了一个围栏来放养羊群,以防止它们被狼侵害,但我们不知道在围栏中是否已经有狼。
从三次数学危机解决的途径可见,前两次解决方案使得数学知识网络系统增加了节点,而第三次却是限制这个网络系统的扩张。由此可见,这个网络的自然扩张不仅有奇点,而且有边界。
五、局部可读性与推理工具的关系
前面明确强调,我们讨论的推理型知识网络必须具有自然人的局部可读性。解决“不可读”问题最高明的办法是人的智力,除此之外只能把知识网络中的一个节点扩张为一系列节点,用时间解决问题。注意到在给出“可读性”定义的时候,我们没能够约定人类使用推理辅助工具的类型。事实上,这是前面留下的不容忽视的“漏洞”,它已经造成了许多高技术工具参与到“推理辅助工具” 的行列之中,包括计算机和人工智能的一系列前沿科技。计算机和人工智能把一系列逻辑推理压缩在一次逻辑推理里,造成了自然人的“不可读”。对这种借助推理工具代替“可读性”的做法你可以不喜欢,你可以不理睬“四色猜想” 和“求堆积猜想”的机器证明,但对“不可读”的新冠疫情预测你却不得不接受,因为全世界都在关心新冠疫情啥时能结束?回答这个问题当然不能通过几年,甚至几十年的逻辑推理来完成。

大家知道,做出疫情预测最为关键的一步是要建立数学模型,然后加以计算求解。历史上,正是依靠数学对于传染病的模型化研究,人类才对其传播模式和严重危害有了更为深刻的理性认识。计算技术和人工智能的快速发展为这一求解带来了划时代的新机遇。新冠病毒肺炎疫情发生以来,我们经常会听到一些专家或机构根据他们的模型预测了疫情终结的大概时间。这里所说的模型就是针对疫情的实际而修正、提炼、选择的数学模型。这个听起来高深莫测的数学模型,原理其实并不复杂。以SEIR 模型为例:如果用 S 代表易感者,也就是可能被传染但还没有感染的人;用 I 代表感染者,即已经被传染但尚未死亡的人;用 R 代表移除者,他们被感染后痊愈或者因病死亡。用 E 表示潜伏期人群。如果用 β, δ, γ, α 依次表示 S 转化为 E,E 转化为 I,I 转化为 R,E 转化为 R 的比率,则其微分方程如下:


疫情预测工作的关键是采集、处理和修正参数 β,δ, γ, α。这一工作既涉及到传染病的医学特点,也涉及到大数据的采集和处理质量,需要处理大量“不可读”的逻辑推理问题。
网上有个号称科学版的印度疫情走向预测(SEIR模型),据说是一个刚毕业的大学生完成的。该预测称,如果印度政府不加干预,印度全国感染人数将达到 11.5亿,死亡 4500 万人;如果政府从 2020 年 3 月 20日开始干预,感染人数可以控制为 5 万,死亡人数控制为 1000;如果政府从那日开始严格干预,感染人数可控制在1.3 万,死亡人数仅 300。我国钟南山教授团队发表的研究工作,对公共卫生干预措施下中国 COVID-19 疫情趋势进行了优化 SEIR模型和 AI 预测,结论是中国的疫情在 2020 年 2 月底已达到峰值,到 4月底将趋于平缓。伦敦帝国理工有预测报告,主要结论是:如无任何控制措施,在 3 个月后到达顶峰时英国将死亡51 万人,美国将死亡 220 万人。ICU病床会在 2020 年 4月第二周达到满负荷。在爆发最高峰期间,需求量将会 30
超出英国目前的 ICU病床量。
面对这些预测,公众关心的问题是哪个预测更准确?而不是逻辑推理的“可读性”。事实上,从数学模型、数据处理、计算程序,到快速计算、结果修正拟合,这是一个非常长的逻辑推理链条,任何自然人的生理功能都不可能窥其全貌。因此,在不得不之中,公众只能相信学术权威。

本文摘自:《数学文化》第12卷第3期 2021
注:本文图片取自 https://image.baidu.com/ 或 https://m.sohu.com/a/155315738614821