原文链接:https://mp.weixin.qq.com/s/kMN8iJBVegUttx418Vk25w
Erik Hoel等人 集智俱乐部

导语
复杂系统内的因果关系可以从不同时空尺度来分析。通常认为,由于微观尺度包含了所有细节,只有在微观尺度才可以完整地表达、量化因果关系,宏观尺度的因果关系只会随附产生,而不能提供更多对因果关系进行研究的可能性。事实真的如此吗?对于复杂系统,是否有可能在更宏观的时空尺度上对其进行分析或建模,反而更有利于捕捉因果关系?在发生因果涌现时,确实如此。
2013年,Erik P. Hoel等人在论文《量化因果涌现表明,宏观可以战胜微观》中,基于信息论定义了一种对因果关系的度量方法,即“有效信息”(effective information),并对简单系统在微观和宏观尺度上分别计算其有效信息。结果发现,当粗粒化处理后的宏观机制相比于底层微观机制具有更高的有效信息,也就是发生因果涌现时,宏观尺度上的模型可以更有效地对系统中的因果关系进行建模。本文是对该论文的全文翻译。
集智俱乐部因果涌现读书会对这篇论文进行了解读,深入探讨了因果涌现理论。详情见文末,欢迎感兴趣的朋友报名加入。
研究领域:因果涌现,时空尺度,有效信息,粗粒化
Erik P. Hoel, Larissa Albantakis, Giulio Tononi | 作者
赵婷婷 | 译者
梁金 | 审校
邓一雪 | 编辑

论文题目:
Quantifying causal emergence shows that macro can beat micro
论文链接:
https://www.pnas.org/content/110/49/19790
目录
摘要
一、引入
二、因果涌现理论
三、结果
四、延伸讨论
五、总结
摘 要
复杂系统内的因果关系可以在多个时空尺度上进行分析。例如,对大脑的分析空间上可以包括在神经元、神经元群和区域水平上的分析,时间上可以跨越数十、数百或数千毫秒。普遍认为,一旦微观尺度的模型表达或系统行为可以被确定,那么在宏观尺度也会相应确定,这种关系被称为“随附性”(supervenience)。
尽管宏观尺度的系统行为的描述可能很方便,但是过去的很多研究都假设,只有在微观尺度才可以完整地表达、量化因果关系,因为微观尺度包含了系统的所有细节,所以在宏观尺度上并不会有更多的对因果关系进行研究的可能性。然而,我们需要在给定一种因果关系量化度量方法的前提下,才可以进一步对上述假设的正确性进行评估。
这里我们定义了一种对因果关系的度量方法,即“有效信息”(effective information, EI),它取决于对系统运行机制描述的有效性及其状态空间的大小:如果对系统运行机制进行描述的方法可以捕捉系统中可能出现的过去和未来状态的程度越高,该描述所处的时空尺度的有效信息就越高。在给定系统微观运行机制的前提下,通过对简单系统在微观和宏观尺度分别计算其有效信息,我们发现,对于某些系统内置的因果结构,有效信息可以在空间或时间的宏观尺度上达到峰值。当粗粒化处理后的宏观机制相比于底层微观机制具有更高的有效信息(即更高的确定性或更小的简并性),以至于超过较小的状态空间,宏观尺度上的模型可以更有效地对系统中的因果关系进行建模。
因此,尽管宏观尺度系统的运行机制是在微观尺度的运行机制的基础上随附产生的,但它可以在因果关系分析方面有效地取代微观尺度的系统运行机制,从而导致因果涌现(causal emergence)——即从微观尺度迁移到宏观尺度分析时获得的有效信息的增益。
一、引入
在科学界,通常认为,如果能更好地描述一个复杂系统的详细因果机制,就能更好地理解该系统的运行机理。有时,求助于“宏观”级别的描述可能对研究系统的因果机制是更有效的,其原因有两个方面。一方面,有些系统在某些 “微观”尺度的状态数据是不可获取的。另一方面,有些粗粒化的模型可能反而更符合对该系统因果机制进行分析的最终目标。然而,从直觉上来说,若需充分理解一个系统的运行机理并准确预测其行为,似乎需要对微观尺度上的因果作用机制有更充分的理解。例如,大脑可以从宏观尺度上的脑部区域和路径、中观尺度上的局部神经元群体,或微观尺度上的神经元和突触来表征[1]。为了对大脑作为一个完整的机体进行理解,科学家启动了以对大脑的微观尺度进行建模为目标的研究项目[2]。
科学研究中广泛使用的还原论方法不仅在实践中取得了成功,也得到了强有力的理论论证的支撑。主要的观点源于一个直观的概念,即当给定一个系统的微观物理机制时,它的所有宏观尺度的行为也相应地可以被确定——一种被称为“随附性”的关系[3]。反之,通常认为这种关系意味着微观机制在最大的程度上决定了系统中的因果关系,也就是说,微观尺度是因果完整的。依据上述观点,在宏观尺度上研究系统中的因果关系似乎并不能做出更多贡献;否则,就会有“多重因果关系”存在[4]。这种逻辑下的“因果排除”论点也经常被用来反驳心理因果关系超越生理因果关系的可能性[5],但它也可以扩展到所有具有随附性的情况,包括不同学科之间的层级关系[6]。
然而,有些不同的观点认为,从微观到宏观的因果涌现是有可能发生的。比较典型的例子包括生物群的行为[7]、蚁群的行为[8]、大脑[9]和人类社会[10]。大多数支持因果涌现的研究工作都是基于定性的分析[11]。一个令人信服的因果涌现的实例需要量化地证明在宏观尺度比微观尺度能更有效的描述因果关系(即“因果涌现”)。到目前为止,为数不多的定量描述系统中的涌现行为的研究中[12]尚没有针对因果模型开展的工作。并且,也尚未研究清楚是哪些因素决定了一些系统中存在因果涌现,而另一些系统则在微观尺度展现更有效的因果信息。
这里我们利用简单的仿真系统,包括神经元系统,定量地表明宏观尺度可以因果地取代微观尺度,即可以发生因果涌现。为了做到这一点,我们通过给每个系统可能的因果状态库施加扰动,并使用“有效信息”(EI)[13]来评估由此扰动产生的影响。有效信息是因果相互作用的一般度量,因为它用扰动来捕捉系统机制相对于其状态空间大小的有效性或选择性。在后文中,将进一步讨论,对于确定性高且简并性低的系统,其有效信息更大,并且会随着噪声(导致因果发散)和/或简并(导致因果收敛)而减小。
对于每个系统,我们在微观尺度上完全描述了因果机制,确定了在任何宏观尺度上可能发生的情况(随附性)。宏观尺度是通过在空间和/或时间上对微观元素进行粗粒化来定义的,这种映射在每个尺度上定义了其可能的原因和结果集合。通过比较不同尺度上的有效信息,作者发现,根据系统的组织方式,因果相互作用可以在宏观而非微观的时空尺度上达到峰值。因此,即使宏观在微观之上随附而生,宏观尺度在因果关系的分析上也可能优于微观尺度。评估系统粗粒化或细粒化引起的有效信息变化提供了一种直接的量化因果涌现和因果退化(causal reduction)的方法。
二、因果涌现理论
下面介绍因果涌现的理论分析部分。我们考虑了由互相关联的二值化(二态)微观元素组成的离散系统S,该系统的逻辑函数(内在因果机制) 作用于其输入信号上。我们首先引入一个关于状态的因果关系的度量,即单个系统状态的“原因信息”和“结果信息”。在此基础上,定义了描述系统S的不依赖于单个状态的系统层面的“有效信息”。
1、关于状态的因果分析。系统S的微观机制给定了其在微观时间步长t上从状态到状态的转移概率矩阵(transition probability matrix, TPM)。基于由Judea Pearl提出的用于因果分析的施加扰动的方法论([14];另见参考文献[18]),转移概率矩阵可以通过在t0[13]时刻以相等的概率1/n对系统S中所有可能的n个初始状态施加扰动得到,该扰动可以用“do”函数进行数学表达[do(S=si) ∀i∈1…n]。
用这种方法对系统进行扰动,对应于可能的原因UC的无约束库(等概率分布),并确定在t+1时结果状态的概率,对应于可能的结果UE的无约束库。因此,虽然UC符合均匀分布U[P(s)=1/n,∀s∈S],UE通常是不均匀的。系统的当前状态S=s0既与所有可能造成它的过去状态的概率分布相关联(“原因集SP|s0”,由贝叶斯规则可得),又与所有可能成为其结果的未来状态的概率分布(“结果集SF|s0”)相关联。因此,一个系统的内在机制和当前状态限制了可能的原因UC和可能的结果UE。该系统中因果相互作用的信息度量[15]可以定义为上述有约束分布和无约束分布之间的差异( Kullback–Leibler 散度(DKL)[16] ):
原因信息(s0)=DKL((SP|s0),UC),
结果信息(s0)= DKL((SF|s0),UE).
原因/结果信息取决于两个属性:(1)系统状态空间的大小(备选状态库),因为两者的上界都是log2(n);(2)系统机制在确定系统过去和未来状态方面的有效性。为了将有效性与系统尺寸区分开来,作者定义了以下标准化系数:

“原因系数”描述了通过一个状态可以确定其过去的原因状态的程度,而“结果系数”指出了这种状态用于确定其未来结果的必要性(图1B)。并且,结果系数可以看做是两个指标,即“确定性”和“简并性”,的函数。
结果系数=确定性系数(s0)-简并性系数(s0)
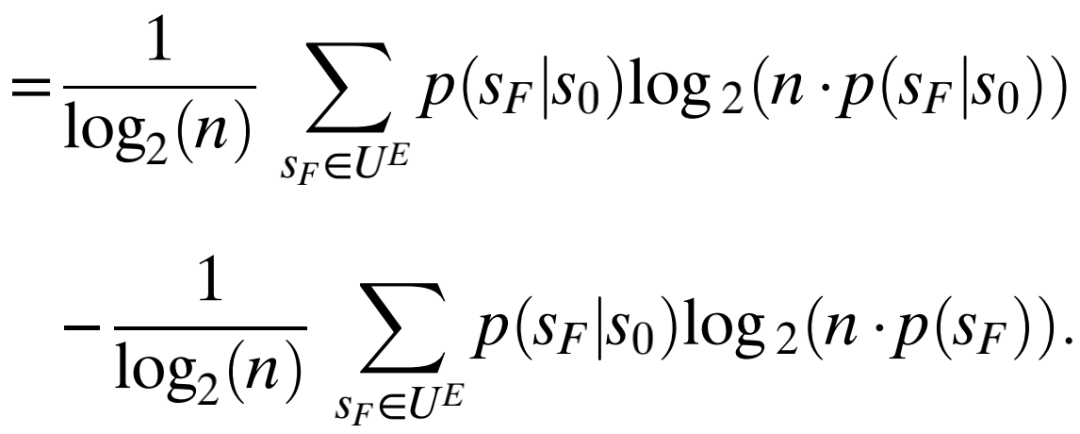
确定性系数是结果库与系统状态均匀分布(U)之间的差,即DKL((SF|s0),U),除以log2(n),它衡量s0在多大程度上确定性地(可靠地)决定了系统的未来状态:如果当前状态以概率为p=1转移至单一未来状态时,其确定性系数是“1” (完全确定性),如果当前状态以均匀概率,即p=1/n,转移至所有可能的未来状态,则其确定性系数是“0” (完全非确定性或噪声)。
简并性系数衡量从其他状态收敛到s0表示的未来状态的确定性程度(即这种状态转移不是由于噪声导致的)。广义上,简并性是指以多种方式确定性地实现相同的结果或功能[17,18]。当由s0确定的未来状态与所有其他状态确定的未来状态都相同时,其简并性系数为1(完全简并性),当s0确定一个唯一的未来状态时,其简并性系数为0(没有简并性)。
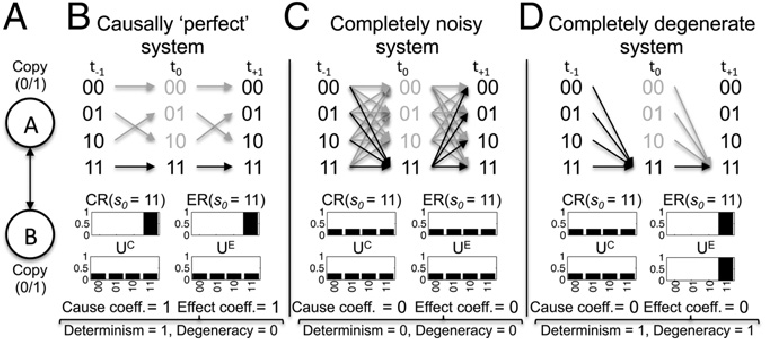
图1. 不同因果机制的案例系统中的因果系数。(A) 系统由两个相互连接的二进制COPY门组成,可能的状态为0和1。(B) 该系统是因果完全的系统,每个状态都有一个确定的原因和一个确定的结果。因此,s0=[11]的因果系数为1。此外,该系统既无发散性(确定性系数=1),也无收敛性(简并性系数=0)。(C) 和(D) 在完全噪声和完全简并性的系统中,状态s0=[11]完全不足以确定系统过去的状态,对于确定系统未来的状态也没有必要的贡献,因此其因果系数=0。需要注意的是,在完全噪声系统中简并性系数为0,因为所有的收敛都是由噪声引起的。
在完全噪声或完全简并性的系统中(图1C和D),原因系数和结果系数取最小值为0,在确定性且非简并性的系统中,其原因和结果系数取最大值为1 [1]。通过分解结果系数,可以很好地说明单个状态对系统的确定性和简并性的贡献。虽然原因系数也反映了系统的简并性和确定性,但这里不作进一步的细分。
2、不依赖于单个状态的因果分析。为了获得系统层面的因果有效性的度量,作者定义了一个不依赖于单个状态的对系统因果机制的基于信息论的度量方法,即通过取所有系统状态的原因信息或结果信息的期望值来获得。该度量被称为有效信息(effective information, EI):
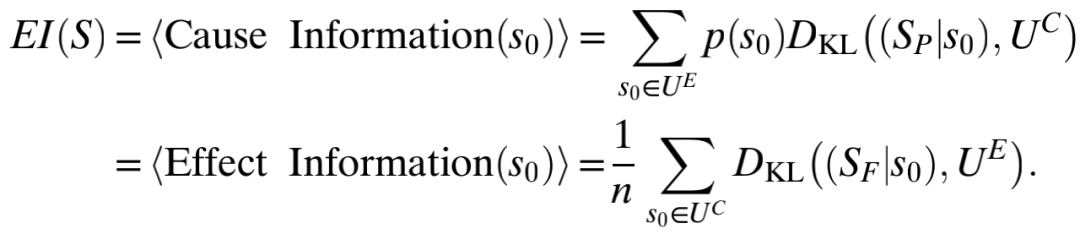
这两项是相同的,因为假设该系统是时间不变系统(即,<t-1→t0> = <t0→t+1>),并且原因信息和结果信息通过贝叶斯规则相互关联。有效信息也是所有可能的原因及其结果之间的互信息(mutual, information, MI),即MI (UC;UE)。
作为因果关系的度量,有效信息描述了原因如何有效地(确定地和唯一地)在系统中产生结果,以及如何从结果中识别产生它的原因的有效性。类似于关于状态的因果度量,系统内因果机制描述的有效性(Eff)也需要将有效信息相对系统的大小进行标准化处理:Eff(S)=EI(S)/log2(n)。类似地,该有效性可以分为两个部分,即确定性和简并性:

因此,给定系统尺寸,系统的有效信息的最大值为1,即Eff(S)=1,并且随着不确定性(噪声引起的发散)或简并性(确定性收敛)而减小,对于完全噪声或简并系统,Eff(S)=0(如图1C和D所示)。
在一个具有完美因果机制的系统中(图1B),每个原因都有一个唯一的结果,每个结果都有一个唯一的原因。因此,这样一个系统(其中Eff(S)=1)是完全可追溯/可预测的,因为从转移概率矩阵(TPM)中不仅可以推断出所有状态的唯一未来轨迹,还可以推断出所有状态的唯一过去轨迹,也称为完全因果可逆性。
3、分析的尺度。一个有限的离散系统S可以从不同尺度上考虑,从最细粒度微观因果模型Sm到各种粗粒度因果模型SM。假设所有宏观尺度SM在微观尺度Sm上是“随附的”,即给定Sm中的微观元素及其之间的因果关系,则{S}的所有其他成员(即系统S的所有可能因果模型集)即可固定[19]。虽然Sm确定SM,但任何SM都可以通过许多不同的低尺度模型来确定,这是一种被称为“多重可实现性”[20]的属性。
4、分组。微观元素为二值化的并用拉丁字母{A,B,C…}表示,宏观元素用希腊字母{α,β,γ… }表示。微观状态被标记为{1,0},宏观状态被标记为{“on”、“bursting”、“quiet”…)。微观元素可以在空间上、时间上或时空上分组归并为宏观元素。微观状态通过映射M: Sm→SM按组分入宏观状态。微观元素的映射必须是穷尽的和互斥的(一个微观元素的所有状态必须映射到同一个宏观元素的状态;同时,只要宏观尺度系统的状态空间减小,宏观元素也可以由单个微观元素构成)。此外,映射必须确保在宏观尺度上没有可用的微观尺度的信息(即分组到宏观元素中的微观元素的标识(identity)将被丢弃)。例如,将两种微观元素的四种状态分组为一种宏观元素的两种状态,即[[00,01,10]= off,[11]= on]是被允许的,而将[[00,01],[10,11]]分组是不被允许,因为区分01和10这两个状态需要知道微观元素的标识。
5、特定尺度的扰动。微观尺度Sm上的因果分析,需要将S等概率地设置为所有可能的微观状态(即测试所有微观的可能性),并确定其产生的结果。当跨到宏观尺度SM进行分析时,S必须以等概率设置为所有可能的宏观状态(即测试所有宏观可能性)。因此,要对任何宏观状态进行因果分析,需要将S设置为所有nmicro个微观状态{sm},而这些微观状态被分组为相应的宏观状态,并对其影响进行平均。上述效果是通过使用“宏观扰动”操作实现的,即![]() 。利用这种宏观扰动,可以得到Sm的每一种粗粒化实现的因果信息和有效信息。每个宏观尺度上的有效信息相当于一系列宏观原因及其宏观结果之间的MI。
。利用这种宏观扰动,可以得到Sm的每一种粗粒化实现的因果信息和有效信息。每个宏观尺度上的有效信息相当于一系列宏观原因及其宏观结果之间的MI。
6、因果涌现/退化。最后,通过评估Sm的所有粗粒化实现上的EI(S),可以提出一个问题,即在{S}的哪个尺度上的因果关系度量能够达到最大值。至此,提供了因果涌现的解析定义,用比特表示为CE=EI(SM)-EI(Sm)。
因此,如果EI(S)在宏观SM,而不是微观Sm上取最大值,则CE>0,从而发生了因果涌现。如果对每个宏观尺度CE<0,则该系统具有因果退化的特性。虽然,这里讨论的重点是相对于微观尺度Sm的涌现/退化,但上述方法也可以用来对不同的宏观尺度进行比较分析。
如上所述,EI(S)既取决于系统状态库的大小,也取决于其因果机制的有效性。当系统从一个尺度跨到另一个尺度时,这两项因素都会随着状态空间的变大或变小而改变,单个状态相对于过去的可回溯性可能增加或减小,相对于未来的确定性也可能变大或变小。系统状态库的大小和因果机制的有效性对ΔEI(S)的信息贡献可以分别表示为: ![]() ,
, ![]() ,其中nm/M为Sm/M的状态库大小。由此可见,
,其中nm/M为Sm/M的状态库大小。由此可见,![]() 。正的ΔIEff可能是由于宏观尺度的描述减少了微观尺度描述的简并性,增加了其确定性,或者两者都有。值得注意的是,将微观尺度的Sm粗粒化为宏观尺度的SM意味着ΔIsize总是负的。因此,只有当有效性ΔIEff的增加超过的ΔIsize减少时,才会发生因果涌现,即 EI(SM)>EI(Sm)。
。正的ΔIEff可能是由于宏观尺度的描述减少了微观尺度描述的简并性,增加了其确定性,或者两者都有。值得注意的是,将微观尺度的Sm粗粒化为宏观尺度的SM意味着ΔIsize总是负的。因此,只有当有效性ΔIEff的增加超过的ΔIsize减少时,才会发生因果涌现,即 EI(SM)>EI(Sm)。
三、结果
我们使用定制的Python程序对系统的所有粗粒化方式进行了因果分析(图中仅显示了EI(S)最大的SM),并使用MATLAB绘制分析结果图。下面,将分别以空间、时间和时空涌现为例进行阐述。
1、空间因果涌现。以一个由四个二值元素Sm={ABCD}组成的系统(如图2A) 作为例子阐释空间因果涌现原理。每个微观机制都是一个作用于两个输入信号的与门,并在一些系统固有噪声的影响下工作。以相同的概率将系统设置为从[0000]到[1111]的所有可能的微观状态,进而构建一个16×16的Sm的转移概率矩阵(即TPM,如图2B)。在微观尺度Sm上,有效信息EI(S)=1.15比特(有效信息的最大取值为4比特), 其有效性Eff(Sm)=0.29。宏观尺度SM (如图2D所示)是微观尺度Sm的粗粒化,如图2B中的映射M所示,该宏观尺度由两个元素{α,β}构成,每个元素都有[“开”“关”]两个状态。通过以相同的概率将系统设置为从[关,关]到[开,开]所有可能的宏观状态得到4×4的SM转移概率矩阵(如图2E)。宏观尺度的有效信息为1.55比特,高于微观尺度的1.15比特。因此CE(S)=0.40比特,说明在这种情况下宏观SM战胜微观Sm,构成了系统S的最优因果模型。这是因为Eff(SM)=0.78,说明SM的转移概率矩阵更接近完全有效性,通过粗粒化获得了有效性的增加比特超过了状态空间大小的损失 - 0.57比特。在这个例子中,在宏观尺度上的有效性的获得主要(其中的91%)来自于噪音的消除(确定性系数(Sm)=0.34;(SM)=0.78),少部分(其中的9%)来自于简并性的降低(简并性系数(Sm)=0.05;(SM)=0.006)。
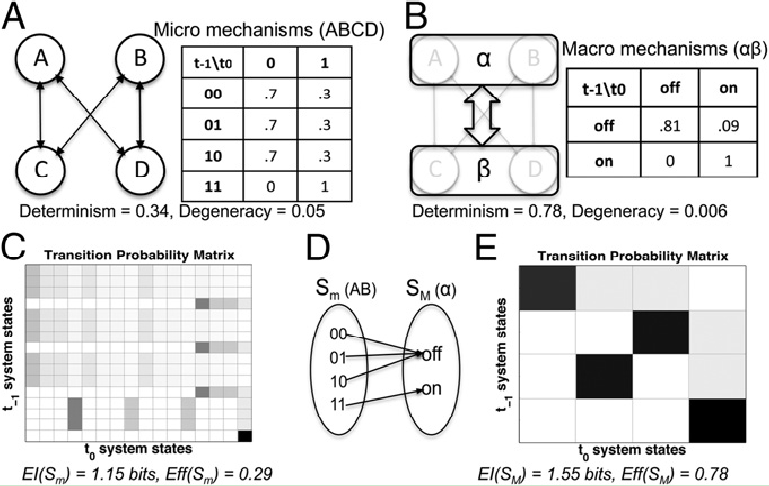
图2. 空间因果涌现(提升确定性)。(A) 系统S的微观尺度Sm由相同的微观机制构成。(B)一个宏观因果尺度SM和它的TPM,该粗粒化由映射M定义(AB到α和CD到β对称)。(C) 微观转移概率矩阵。(D)SM及其宏观机制。(E)虽然状态空间的尺寸减小,但是通过提升确定性和提高有效性Eff,宏观的有效信息高于微观的有效信息。
在状态相关的情况下比较SM和Sm,宏观尺度更高的有效性也是显而易见的。例如,将状态{ABCD}=[0001]下Sm的因果分布与图3中对应的SM状态{αβ} = [关,关]进行比较。计算Sm=[0001]的因果分布与无约束库的距离(通过DKL定义),得出0.83比特原因信息和0.43比特结果信息。对于宏观SM,原因信息为2比特,结果信息为1.35比特。宏观胜过微观,因为{αβ}=[关,关]比{ABCD}=[0001]更具有选择性,也具有更高的可靠性。
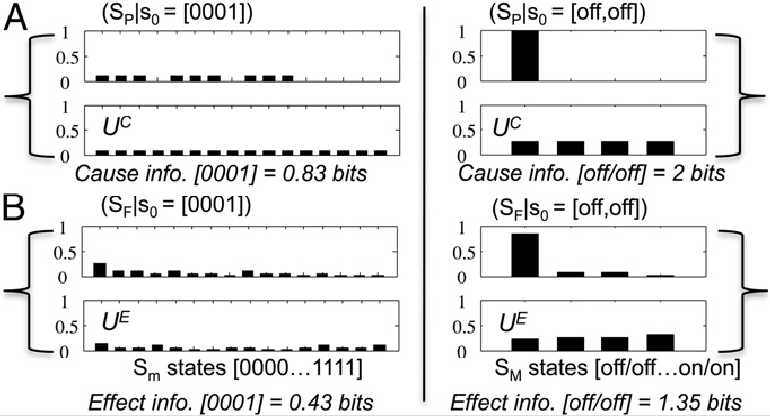
图3. 关于状态的因果信息。(A)微观状态{ABCD}=[0001]的Sm原因信息被计算为原因状态库[0001]和非约束微观状态库UC(左)之间的距离(通过DKL定义)。随附的宏观状态{αβ}=[关,关](如右半图所示)的SM原因信息是原因库[关,关]和非约束宏观库UC之间的距离(通过DKL定义)。(B)结果信息。宏观尺度更高的因果信息是由于确定性的增加和简并性的减少,表现出了更高的选择性。
因果涌现可能不仅来自确定性在宏观尺度的增加(如上所述),也可能来自简并性的减少。在图4中,微观元素A-F是通过具有确定性的与门进行连接的,并且该系统具有高简并性(如图4A,确定性系数=1;简并性系数=0.6),导致Eff(Sm)=0.4,EI(Sm)=2.43比特(如图4C)。一种较好的对该系统进行粗粒化的方式是在宏观尺度上将六个微观与门分组成为三个宏观复制门(即αβγ)(如图4B)。宏观和微观都是确定性的,但是通过消除简并性。从而得到,Eff(SM)=1比特,EI (SM)=3比特,该粗粒化下发生了宏观因果涌现 (CE= 0.57比特)。
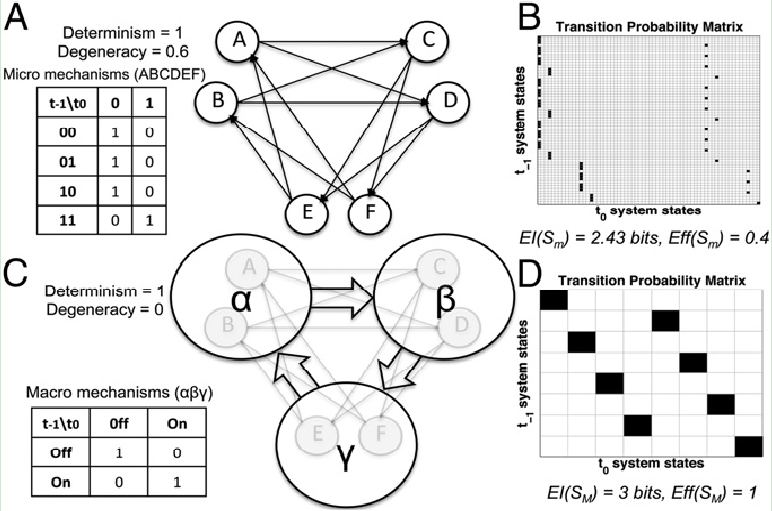
图4. 空间因果涌现(减少简并性)。(A)有确定性与门的简并性系统Sm。(B)宏观上,与门的循环连接被映射到复制门的循环连接上。(C)确定性但简并的微观转移概率矩阵。(D)具有零简并性的确定性宏观转移概率矩阵。通过减少简并性达到完美有效性,宏观尺度上的因果有效性战胜了微观尺度(CE=0.57比特)。
2、时间因果涌现。对空间上的微观状态进行分组的原理也可以推广至时间维度上。时间分组将微观时间步(tx) 粗粒化为宏观时间步(Tx)。如图5所示,对于系统的输入和响应,都可以将两个相邻的时间步粗粒化为一个时间步。因此,元素在输入和输出上可以表达为一个二阶马尔可夫机制(如图5A)。如图5B所示,在一个微观时间步上评估的因果相互作用很弱(EI(Sm)=0.16比特;Eff(Sm)=0.03),因为它们未能捕获二阶机制。相比之下,对两个微观时间步聚合后的因果分析 (如图5C) 可以得到EI=1.38比特,Eff(Sm)=0.34。其中,从微观到宏观的时间分组划分α={At, At+1}和β={Bt, Bt+1} (如图5D) 类似于图2中的空间分组:{00, 01, 10}={关}和{11}={开}。在宏观时间步上,系统变得完全确定性和非简并性,EI(SM) = 2比特,Eff(SM) = 1,CE(S) = 0.62比特(如图5E和F所示)。
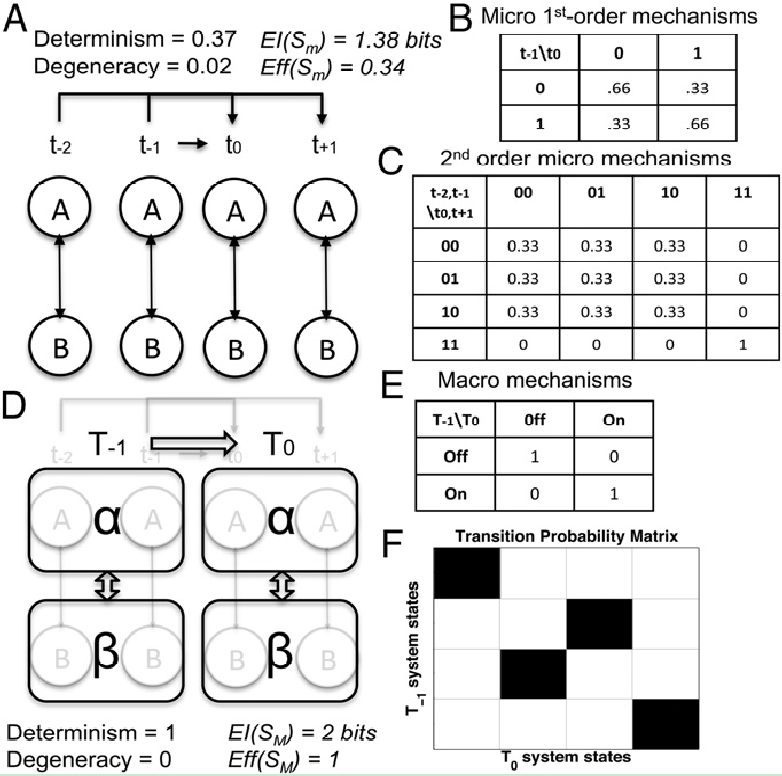
图5. 时间因果涌现。(A)Sm由二阶马尔可夫机制A和B构成:t0时刻,每个机制基于t-2和t-1时刻的输入在t0和t+1时刻做出输出反应。(B)在微观时间步上的因果分析提供了一个不完全因果的系统视角。(C)两个微观时间步上的因果分析表示为一个二阶马尔可夫机制。(D)最优宏观系统SM为将两个微观时间步分组为一个宏观时间步,从而得到宏观元素{α,β}。(E)每个粗粒化的宏观机制有效地对应于一个确定性的复制门。(F)一个宏观时间步的转移概率矩阵的Eff(SM)=1,两个微观时间步的转移概率矩阵的Eff(Sm)=0.34;CE=0.62比特。
3、时空因果涌现。一般来说,涌现可能在空间和时间上同时发生(如图6所示)。如图6A所示,9个类似于神经元的元素为二阶马尔科夫机制,每个元素都分别在两个微观时间步 t-2 t-1和 t0 t+1上对输入进行聚合并产生输出。此外,在上面的例子中,宏观元素中的微观元素之间没有连接,并且是因果等价的。为了证明这不是因果涌现的必要条件,在图6中,微观元素是完全连接的,并且是因果异构的(在图中没有绘制元素的自连接)。所有元素以不同的概率自发活动[1]:p(A/D/G)=0.45;p(B/E/H)=0.5;p(C/F/I)=0.55。由于不同的组内和组间机制,元素被构造为三组{ABC,DEF,GHI}:在每个组内,如果组内连接的总和为0(对于两个时间步),则所有元素保持0 (对于接下来的两个时间步)。然而,如果在两个时间步上来自另外两个组中的一个或两个组间连接的总和为6 (即发生了同步活动),则p(1)在接下来的两个时间步中被提高0.5。在宏观尺度SM上 (如图6B所示),三组神经元分别组合成为宏观元素,两个微观时间步(tx))被分组为一个宏观时间步(Tx)。
用神经元术语来说,这些宏观元素可以表示具有三种状态的“微柱”:“抑制的” (所有微柱神经元在Tx)时安静),“接受的” (部分微柱神经元在Tx)时放电),或“爆发的” (所有微柱神经元在Tx)时放电)。宏观因果相互作用可以总结如下:如果一个宏观元素被抑制,只有接收到一个爆发才能将其转移到接受状态,或以更低的可能性转移到爆发状态;否则,它会保持被抑制的状态。类似于在前面的例子中,粗粒化后的SM比Sm (EI(Sm =0.59比特;Eff(Sm)=0.033)有着更高的EI(SM)=3.51比特和Eff(SM)=0.74。在这种情况下,时空因果的涌现 (CE(S)=2.92比特) 是由于系统确定性的增加,其程度远远超过了系统简并性的轻微增加和状态集大小的减小。
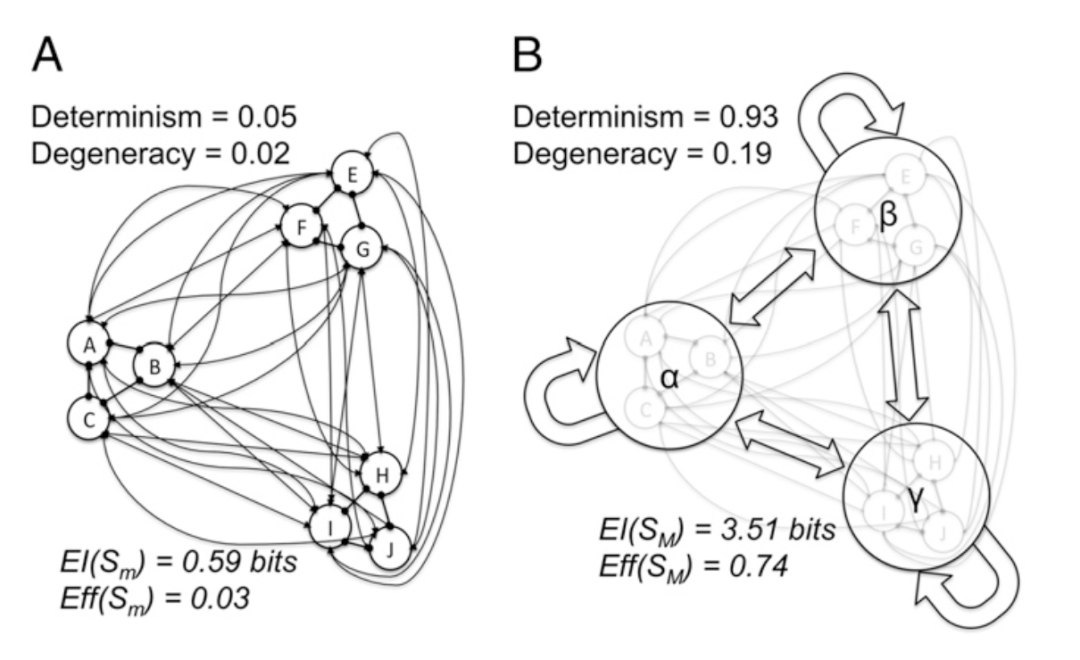
图6. 时空因果涌现。(A)“神经元”系统融合了图5中系统的时间特征和与图5不同的空间结构。规则箭头和圆形箭头分别表示组间和组内连接。(B)每个宏观元素接收来自自身和其他宏观元素的输入。宏观尺度因果有效性胜过微观尺度,导致时空因果涌现[CE(S)=2.92比特]。
四、延伸讨论
本文提供了一种用于评估系统内因果相互作用关系在哪个时空粒度达到最大值的原则性分析方法。因果相互作用通过有效信息(EI)进行评估,有效信息对系统机制的有效性和状态空间的大小都很敏感。仿真系统的实例表明,在空间和时间上对微观机制进行粗粒化后,EI在宏观尺度上高于微观尺度。在这些情况下,宏观机制相较于微观机制,可以更好地对系统内的因果关系进行描述。
1、有效信息、有效性和涌现。EI对应于乘以用比特进行表示的库的大小的系统机制“有效性”。有效性Eff(S)是所有系统状态下的结果系数的平均值。结果系数衡量当前系统状态对于确定未来系统状态时在多大程度上是必需的。并且,这个指标是关于决定性减去简并性的函数。在原因方面,与结果系数等价的是原因系数,它衡量当前状态在多大程度上足以指定系统过去的状态。对于给定的当前状态,原因与结果系数可能不同:例如,一个当前状态可能有许多原因,但只有一个结果。结果系数对所有可能的系统状态的平均值,即有效性,对应于原因系数的平均值,即由其对应的结果的概率进行加权平均。换句话说,在一个时间不变的系统中,原因的平均选择性对应于结果的平均选择性。其他的类似于EI的因果关系的度量,如果可以反映系统的因果结构(选择性、确定性、简并性)和系统的规模,那么该度量方法理论上讲也可以发现因果涌现的现象。
仿真实验的主要结论是,在空间或时间上的粗粒化操作都能产生较高的EI值。尽管根据定义,对于EI而言,微观的状态空间比宏观的更大更具优势,但因果涌现依然会发生。考虑到微观的固有优势(状态空间大),不难理解为什么原有的用于分析系统的研究方法是基于还原论的。但是,上面给出的例子表明,如果宏观获得了更大的信息有效性增益,那么由于宏观规模较小而造成的EI的固有损失可以被抵消。从而,在宏观机制(宏观机制是由底层的微观机制构建而成的)中可以获得更大的有效性,前提是在宏观尺度上,确定性增加和/或简并性减少。当在最优宏观尺度上EI (CE>0)获得增益时,就发生了因果涌现。反之,如果EI出现损失 (CE<0),发生了因果退化,并且微观尺度是因果分析的最佳尺度。这里的因果分析方法指出,原有文献中的定性分析方法或者非因果的涌现分析方法不能够支持因果涌现的研究,即研究宏观尺度如何,以及为什么能够比微观尺度具有更大的因果有效性[22,23]。
2、微观宏观映射和备选方案集。基于有效信息可以公平地在微观和宏观尺度对系统中的因果关系进行比较分析。在这项工作中,仿真算例的设计遵循以下原则:首先,宏观机制严格地随附于微观机制,即一旦定义了微观机制,所有宏观机制都随之确定。也就是说,不在宏观尺度增加额外的只适用于宏观的体现因果关系的规则[24]。并且,从微观元素至宏观元素的映射,不会对微观元素的标识进行保留,否则,宏观尺度将获得微观尺度的状态标识,从而抵消宏观尺度状态空间减少的效果。最后,对因果关系进行评估时,在微观和宏观尺度上假设所有可能的扰动状态呈相互独立的均匀分布。对于宏观尺度,为了实现其扰动的均匀分布,宏观状态所对应的底层微观状态的扰动概率须通过微观状态到宏观状态的映射关系进行修正。修正的微观扰动分布在宏观尺度呈现均匀分布的扰动,并使得EI对每个相应尺度上的因果结构更加敏感,最终产生宏观EI超过微观EI的现象。
3、作为系统固有属性的涌现。EI是一种因果度量,它需要以各种可能的方式对系统施加扰动,并评估扰动对系统产生的影响。同时,它也是一种信息度量的方法,因为它的值取决于系统中状态备选集的大小。事实上,在这里提出的方法论中,因果关系和信息是必然联系在一起的[25],因此才有了“有效信息”这个术语。并且,度量EI的过程帮助我们揭示了系统的一些“固有”属性,即系统对其本身所有可能的状态的平均有效性或选择性。有效性或选择性可以在多个时空粒度中进行评估,而EI在哪个时空粒度达到最大值又是由系统的固有属性决定的。这并不妨碍研究者在其他宏观尺度、微观尺度或同时在多个尺度对系统开展有益的研究(例如,神经科学家在离子通道、单个神经元、局部场电位或功能性磁共振信号层面研究大脑)。然而,因果涌现意味着,具有最高EI的宏观尺度是最适合描述、预测和倒推系统行为的时空尺度[26]。
对使得EI最大的宏观尺度的探索在信息论中有一个可以类比的研究内容:信道容量是通信系统的一种内在属性,被定义为通过搜索所有可能的输入信号的分布,可以在信道中以一定速率传输的最大信息量[27]。寻找最优时空粒度的因果涌现是基于类似的搜索策略,但两者也有几点不同。首先,EI是通过对系统本身的扰动来评估的,而非一个通道,即系统既是它自己的输入也是它自己的输出。其次,微观状态上的概率分布必须与微观元素到宏观元素(或聚合后的时间间隔)的适当映射相互对应。因果涌现与其他现有的度量方法之间的联系,如可逆性,马尔可夫过程中的汇集[28],机器 [29]等,都是未来值得扩展的研究方向。
4、因果排斥及其含义。这里提出的因果分析既支持随附性(即在宏观尺度上没有额外的因果机制引入),也支持因果排斥(Causal Exclusion),即对于给定的系统在给定的时间,因果只在一个尺度上发生,否则因果关系将被重复多次计算[4]。然而,因果分析也表明,取决于系统的因果机制,实际上其EI也有可能在宏观尺度上取最大值。在这种情况下,因果排斥完全颠覆了还原论的假设,因为为了避免重复计算因果,最优的宏观因果关系必须排斥微观因果关系。也就是说,宏观机制总是由构成它的微观机制决定的(附随性);但如果发生了因果涌现,宏观的因果并不能还原为微观的因果,在这种情况下,宏观的因果战胜了微观的因果并取而代之。各尺度之间不可还原性的概念(即宏观是否可以打败微观)与一个尺度内元素子集之间不可还原性的概念(即整体是否可以大于其部分[15, 25])互为补充。从系统的角度来看,涌现(CE>0)意味着在最优宏观尺度上的因果“自我定义”——在这个尺度上,它的因果相互作用更为“聚焦”[30],并且对系统的干预也更为有效。
5、对真实系统的适用性。若在所有微观/宏观尺度上穷尽地测量EI,对于复杂的物理或生物系统是不现实的。然而,从上述分析可以得出一些有益的指导原则:(i)如果EI(Sm)≥EI(SM),则因果涌现是不可能发生的,且系统的因果退化成立;(ii)如果EI(Sm)>log2(nM),其中nM是SM的状态库大小,则因果退化成立;(iii)如果对于某些粗粒化过程,Eff急剧增加,则可以重点考察因果涌现是否发生(如果ΔIEff>>−ΔISize )。
因此,在微观尺度上已经接近最大有效性的系统是因果退化的。相比之下,如果系统中存在相互联系紧密且具有自发活动的元素组,同时若能区分组内和组间连接,如图2中所示的简化的神经系统,更有可能发生因果涌现。在真实的神经系统中,可以使用光遗传学和钙成像等工具在不同尺度上度量因果有效信息,例如毫秒间隔内单个神经元的微观尺度,几百毫秒间隔内神经元群的中观尺度,数秒间隔内大脑区域的宏观尺度。这样一来,对一些经典的假说,如皮质微小柱可能构成大脑功能的基本单位[31]等,可以用有效信息度量来开展严格的实验对其进行验证。研究哪些在复杂网络(如大脑)中频繁出现的小组团(small motifs),会决定整个复杂网络是更倾向于因果涌现还是因果退化。针对因果涌现发生的可能性的启发式评估也可依据连接图的分析,它可以给出退化的估计,进而结合对系统内固有噪声的了解,可以进一步提供对确定性的估计。
五、总结
本文提出的方法论为关于因果涌现的直观认识提供了理论支持,即为了弄明白一个系统是如何运作的,应该找到会对系统“造成重大差异(从结果角度)”的差异(从原因角度)[25, 36]。
它还表明,像大脑这样复杂的、多尺度的系统很可能在宏观尺度“运作”。因为在生物系统中,对信息的处理过程中不得不处理不可预测性,而微观尺度的因果关系的减弱[18],即宏观尺度的因果涌现,有利于生物体处理这种不可预测性。这也适用于一些用于补偿噪声和退化的工程系统的设计。
通过这种因果涌现的视角可以更进一步讨论,从微观物理学到宏观经济学的学科体系的层级性组织方式,可能不仅仅是为了方便开展研究工作,而是在相应的组织层次上其探索系统因果机制的收益更大,这也是因果涌现现象的真实写照。